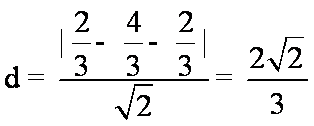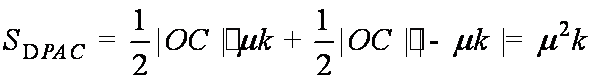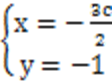- 椭圆的定义及标准方程
- 共573题
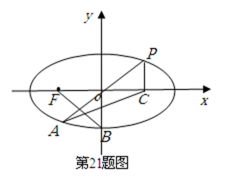
20.已知如图,在平面直角坐标系xoy中,点B

(1)求出椭圆C的方程;
(2)当直线PA平分FB时,求k的值;
(3)当k=2时,求点P到直线AC的距离;
(4)是否存在正实数k使
正确答案
见解析。
解析
(1)因为椭圆C的长轴长为4,点B



(2)由题意可知F为


(3)当k=2时,直线l的方程为

解得P点为



(4)存在正实数k使

可得




所以
因为k(k>0),当且仅当

知识点
20.已知如图,在平面直角坐标系xoy中,点B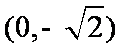
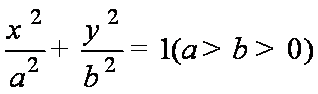
(1)求出椭圆C的方程;
(2)当直线PA平分FB时,求k的值;
(3)当k=2时,求点P到直线AC的距离;
(4)是否存在正实数k使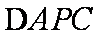
正确答案
见解析。
解析
(1)因为椭圆C的长轴长为4,点B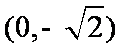
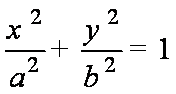
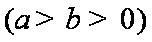
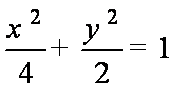
(2)由题意可知F为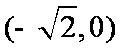
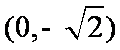
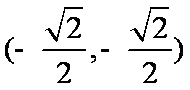
(3)当k=2时,直线l的方程为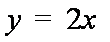

解得P点为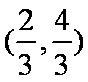
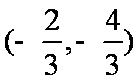
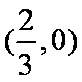
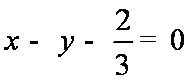
(4)存在正实数k使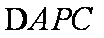
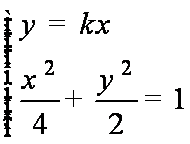
可得

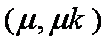
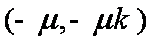
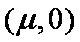
所以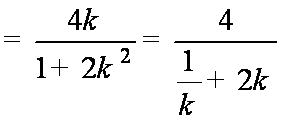
因为k(k>0),当且仅当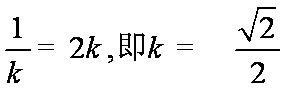
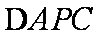
知识点
19.设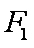
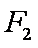
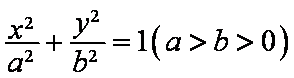
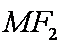
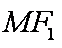
(1)若直线MN的斜率为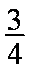
(2)若直线MN在y轴上的截距为2,且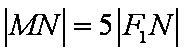
正确答案
见解析。
解析
(1)根据c=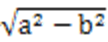

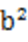
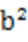
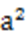
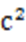
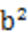



(2)由题意,原点O的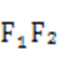
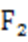
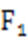
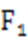

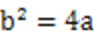
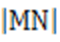
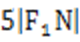
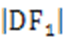
设N(x,y),由题意可知y<0,则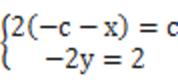
代入方程C,得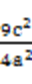

将①以及c=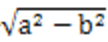
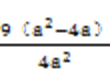

解得a=7,
a=7,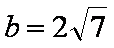
知识点
20.已知椭圆







(1)求椭圆
(2)过定点












正确答案
见解析。
解析
(1)由已知



在


故

于是椭圆

(2)设




假设存在点






因为


因为


整理得
因为



知识点
如图,已知椭圆C:




(1)求椭圆C的方程;
(1) 过点








正确答案
见解析
解析
解:(1)

故椭圆C的方程为
(2)直线MN的斜率必存在,设其直线方程为

联立方程



由


设点R的坐标为



又



知识点
如图,已知中心在原点,焦点在x轴上的椭圆




(1)求椭圆
(2)若满足:


正确答案
见解析。
解析
本小题主要考查椭圆的几何性质、直线与椭圆的位置关系、平面向量等基础知识;考查运算求解能力,推理论证能力等;考查数形结合思想,函数与方程思想,化归与转化思想等,满分13分
(1)依题意可设椭圆

因为离心率

所以




线段AB的方程为
设直线l与直线AB平行与椭圆相切于x轴下方的P点,显然当C点与P点重合时,
△CAB的面积取到最大值。
可设直线AB的方程为
由


令△=
解得

所以直线l方程为
点C到直线AB的距离d等于直线l与直线AB的距离,
即d=
所以△CAB的面积的最大值

(2)设
因为


因为点



将(1)、(2)代人 (3) 得




从而(4)式化为

因为



所以

知识点
已知椭圆




(1)求椭圆的标准方程;
(2)求以


(3)设




求证:线段
正确答案
见解析
解析
(1)由点


故


所以椭圆方程为
(2)以

即


因为以


所以圆心到直线

所以

(3)方法一:由平几知:
直线

由

∴
所以线段

方法二:设
则

又
所以,
知识点
20.给定椭圆






(1)求椭圆
(2)若直线




求
正确答案
见解析。
解析
(1)
(2)



知识点
14.椭圆
正确答案
解析
因为椭圆


知识点
19.已知椭圆C:

(1)求椭圆的方程;
(2)设







正确答案
见解析。
解析
(1)由题意:以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为
∴圆心到直线
∵椭圆

故所求椭圆方程为
(2)由题意知直线


将直线方程代入椭圆方程得:
∴
∴
设

当t=0时,直线l的方程为y=0,此时t=0,
当
得
∴
将上式代入椭圆方程得:
整理得:
由
综上所以t∈(-2,2)
知识点
扫码查看完整答案与解析