- 椭圆的定义及标准方程
- 共573题
复数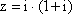
正确答案
解析
略
知识点
如图,点









(1)求椭圆
(2)求

正确答案
(1)
解析
(1)由已知得到


(2)因为直线









由


当
知识点
设F1、F2分别是椭圆E:


(1)求E的离心率;
(2)设点P(0,-1)满足|PA|=|PB|,求E的方程。
正确答案
(1)
(2)E的方程为
解析
(1)由椭圆定义知


直线


设A(




化简得
则

因为直线AB斜率为1,所以
得


(2)设AB的中点为


由|PA|=|PB|,得




故椭圆E的方程为
知识点
如图,椭圆C:


(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由。
正确答案
(1) 
解析
(1)由P

依题设知a=2c,则b2=3c2,②
②代入①解得c2=1,a2=4,b2=3.
故椭圆C的方程为
(2)方法一:由题意可设AB的斜率为k,
则直线AB的方程为y=k(x-1),③
代入椭圆方程3x2+4y2=12并整理,得(4k2+3)x2-8k2x+4(k2-3)=0.
设A(x1,y1),B(x2,y2),则有
x1+x2=

在方程③中令x=4得,M的坐标为(4,3k)。
从而


注意到A,F,B共线,则有k=kAF=kBF,即有
所以k1+k2=

④代入⑤得k1+k2=
又k3=
故存在常数λ=2符合题意。
(2)方法二:设B(x0,y0)(x0≠1),则直线FB的方程为:
令x=4,求得M
从而直线PM的斜率为
联立
得A
则直线PA的斜率为:

所以k1+k2=
故存在常数λ=2符合题意
知识点
如图,点









(1)求椭圆
(2)求

正确答案
见解析。
解析
(1)由已知得到


(2)因为直线









由


当
知识点
已知


(1)当直线

(2)设直线


正确答案
(1)
解析
(1)解:因为直线
所以
又因为
故直线
(2)解:设
由

则由
知
由于
故O为F1F2的中点,
由
设M是GH的中点,则
由题意可知,
好
即
而
所以
又因为
所以
知识点
在平面直角坐标系xOy中,直线l的参数方程为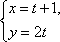
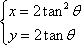
正确答案
(2,2),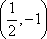
解析
解:因为直线l的参数方程为(t为参数),由x=t+1得t=x-1,代入y=2t,得到直线l的普通方程为2x-y-2=0.
同理得到曲线C的普通方程为y2=2x.
联立方程组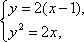
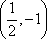
知识点
如图,椭圆C:


(1)求椭圆C的方程;
(2) 求
正确答案
(1) 

解析
(1)由题:
左焦点(﹣c,0)到点P(2,1)的距离为:
由(1) (2)可解得:
∴所求椭圆C的方程为:
(2)易得直线OP的方程:y=

∵A,B在椭圆上,
∴
设直线AB的方程为l:y=﹣
代入椭圆:
显然
∴﹣

由上又有:


∴|AB|=



∵点P(2,1)到直线l的距离为:
∴S



当|m+2|=


此时直线l的方程y=﹣
知识点
已知椭圆






正确答案
解析
略
知识点
20.已知椭圆



(1)求椭圆
(2)设过








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析










































