- 椭圆的定义及标准方程
- 共573题
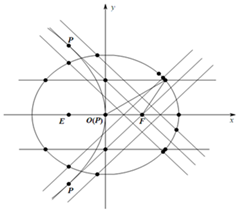
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得
若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由。
(3)过椭圆E上异于其顶点的任一点P,作

正确答案
见解析。
解析
(1)依题意知:椭圆的长半轴长
设椭圆E的方程为
由椭圆的对称性知|OC|=|OB| 又∵
∴AC⊥BC,|OC|=|AC| ∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1) ,
将C的坐标(1,1)代入椭圆方程得
∴所求的椭圆E的方程为
(2)解法一:设在椭圆E上存在点Q,使得

即点Q在直线
∴点Q即直线
∵直线


∴满足条件的点Q存在,且有两个,
【解法二:设在椭圆E上存在点Q,使得

即
又∵点Q在椭圆E上,∴
由①式得

∵方程③的根判别式
∴方程③有两个不相等的实数根,即满足条件的点Q存在,且有两个,
(3)解法一:
设点


∴O、M、P、N四点在同一圆上,
且圆的直径为OP,则圆心为
其方程为
即
即点M、N满足方程④,又点M、N都在
∴M、N坐标也满足方程
⑤-④得直线MN的方程为
令



∴
∴

【解法二:设点
直线PM的方程为

同理可得直线PN的方程为
把P点的坐标代入④、⑤得
∴直线MN的方程为





∴

知识点
已知椭圆



(1)求椭圆C1的方程;
(2)设椭圆









(3)设




正确答案
见解析。
解析
(1)由直线



由


所以椭圆的方程是
(2)由条件,知




(3)由(2),知

∴
由
∵

∴


又
∵


故

知识点
设椭圆
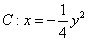
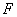
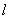
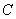
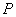
(1)求直线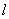
(2)椭圆上是否存在点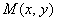
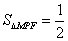
正确答案
见解析。
解析
(1)抛物线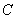
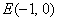
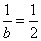
所以,
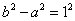

因此,所求椭圆的方程为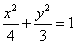
(2)椭圆的右焦点为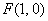
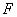
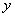
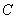


① 若
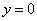
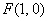
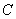
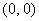
的方程为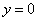
② 若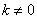

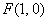
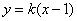
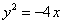
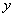
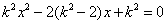
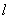
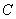
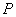
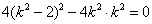
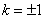
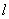
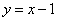


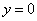
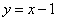

可求出点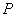
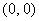
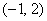
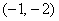
①若点
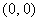
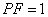
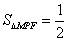
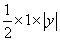

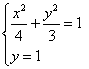
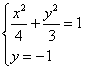
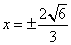
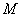
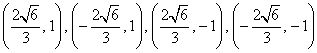
②若点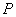
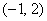
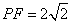
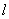
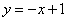
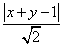
于是有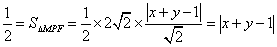
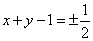
与(*)式联立: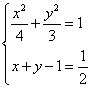

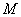
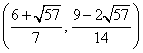
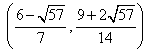


③ 若点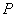
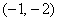
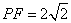
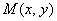

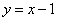
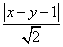
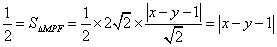
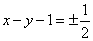
与(*)式联立: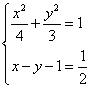

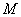
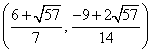
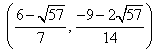
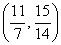
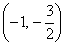
综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点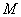
知识点
已知


(1)当



(2)当


正确答案
见解析
解析
(1) 设

因为

又点
所以 

得到 


当

当

{说明:若少一种情况扣2分}
(2)法1:根据题意可知,直线
设直线





联立


由

所以

所以
如果

所以

化简
由②得

化简得 
{此步化简成


故
法2:设


所以 
设


因为

所以,有
因为


所以
所以
知识点
如图5所示,点













(1)求椭圆
(2)在点
(i)设点




(ii)设直线








正确答案
见解析。
解析
(1)由椭圆


动三角形















(2)(i)解法一:设



因为点






易知






即

从而点



令

即



解法二:同解法一求出



消去参数































(ii)解法一: 设




故由



同理可求


从而有

解法二:设直线










因直线



同理可求:

不妨设

于是


又




对于①,②,可视实数


即

对于①,③,可视实数


即

进而有
(亦可由①-②化简得:


易知


从而

知识点
扫码查看完整答案与解析