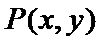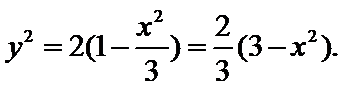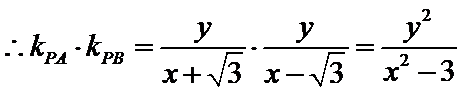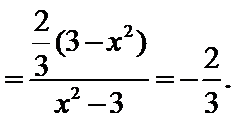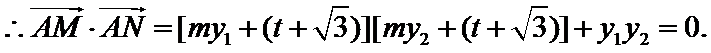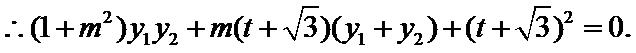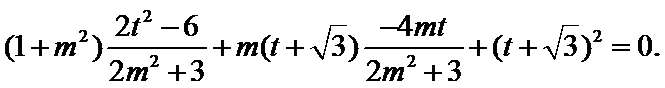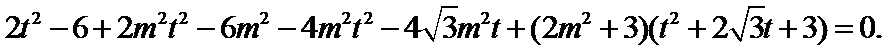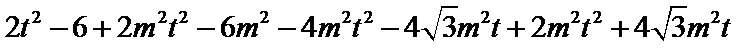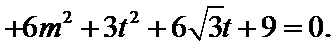- 椭圆的定义及标准方程
- 共573题
已知椭圆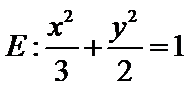
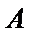
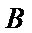
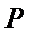
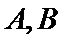
24.求直线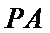
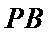

25.设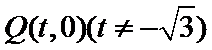

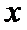
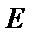

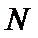
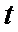
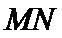
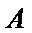

正确答案
直线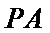
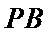
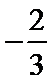
解析
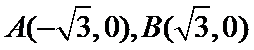
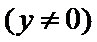
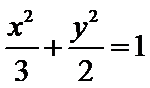
考查方向
解题思路
解题步骤如下:由椭圆的方程,可得到A ,B两点的坐标,设出点P(x,y),即可表示出直线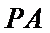
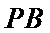
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
正确答案
存在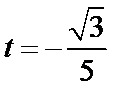
解析
【解析】令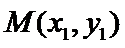
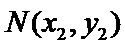
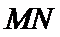
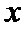
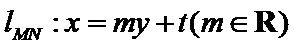
由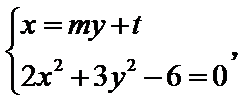
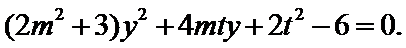
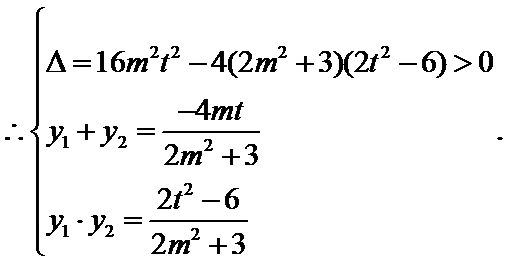
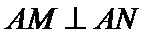
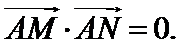
将(*)式代入上式,得
即
展开,得
整理,得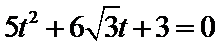
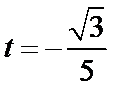
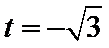
经检验,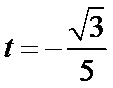
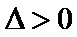
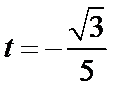
考查方向
解题思路
解题步骤如下:要满足以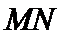
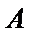

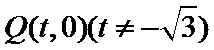
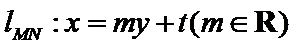
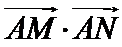
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
已知椭圆

25.求以线段
26.过点







正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

(I)因为


所以以线段

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

则直线



等价于
依题意,直线


由

因为直线


即

设





令

当

所以
化简得,
所以
当
所以存在点

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

已知椭圆

22.求椭圆E的方程;
23.设经过

正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(I)设椭圆E:
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
正确答案
(2)x=4
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(II)将直线



直线AM的方程为

直线BN的方程为

联立得
或

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
已知椭圆


21.求椭圆
22.从椭圆








正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(1)


……4分
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
正确答案
(2)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(2)设点














所以

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
11.已知直线







正确答案
知识点
扫码查看完整答案与解析