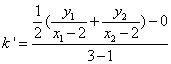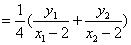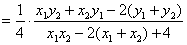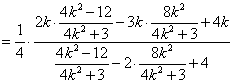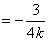- 椭圆的定义及标准方程
- 共573题
已知椭圆C的中点在原点,焦点在


(1)求椭圆C的方程;
(2)已知点

正确答案
见解析。
解析
知识点
已知椭圆




(1)求椭圆
(2)过右焦点















正确答案
见解析。
解析
(1)由条件知
故所求椭圆方程为
(2)设过点




将直线



整理得:
因为点


且
直线



令



直线

将

所以

知识点
已知椭圆
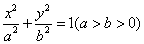


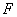
(1)求椭圆
(2)过点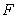
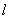
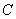
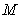
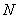

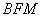
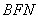
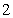
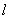
正确答案
见解析
解析
(1)由已知得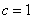

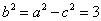

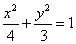
(2)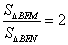
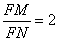
当直线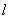

当直线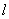

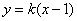
由
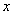
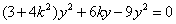
设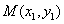
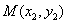

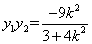
由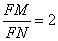
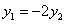
由①②③解得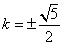
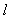
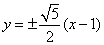
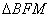
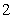
知识点
设椭圆




(1)求椭圆C的方程;
(2)抛物线










正确答案
见解析。
解析
知识点
已知椭圆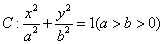
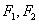
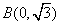
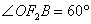
(1)求椭圆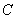
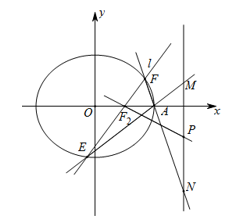
(2)如图,过右焦点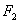
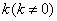
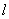
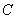
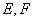
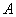
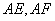
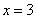
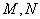
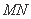
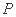
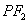
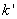
求证: 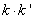
正确答案
见解析
解析
(1)由条件可知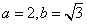
故所求椭圆方程为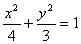
(2)设过点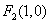
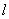
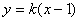
由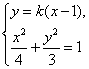
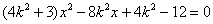
因为点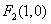
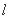
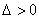
设点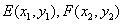
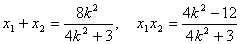
因为直线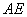
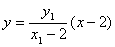
直线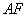
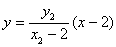
令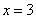
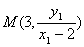
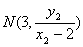
所以点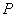
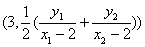
直线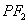
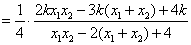
所以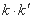
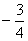
知识点
扫码查看完整答案与解析