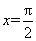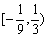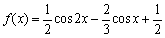- 三角函数与三角恒等变换
- 共3475题
6.偶函数


正确答案
解析

考查方向
解题思路
先平移,然后根据图像关于原点对称求解!
易错点
1、本题易在左右平移时发生错误,易忽视x的系数
知识点
当今全球规模最大的单一金融市场和投机市场是_________。
A.股票市场
B.黄金市场
C.期货市场
D.外汇市场
正确答案
D
解析
暂无解析
城市房屋白蚁防治中,通过在白蚁蛀食的食物中或在白蚁主要出入的蚁路中喷入白蚁药物,使出入的白蚁身体粘上白蚁药粉,药粉通过相互传染传递给其他白蚁,导致整巢白蚁中毒死亡的办法称之为( )。
A.药杀法
B.挖巢法
C.诱杀法
D.生物防治法
正确答案
A
解析
暂无解析
已知函数
15.求
16.若将


求函数

正确答案
详见解析
解析
解 (1)


考查方向
函数y=Asin(ωx+φ)的图象变换;三角函数的周期性及其求法.
解题思路
利用倍角公式及诱导公式化简,然后由周期公式求周期
易错点
计算化简能力弱,三角函数性质掌握不牢固
正确答案
详见解析
解析
(2)由已知得



故当


当


考查方向
函数y=Asin(ωx+φ)的图象变换;三角函数的周期性及其求法.
解题思路
由三角函数的图象平移得到函数g(x)的解析式,结合x的范围求得函数g(x)在区间
易错点
计算化简能力弱,三角函数性质掌握不牢固
已知函数
(1)求
(2)若


正确答案
见解析。
解析
(1)
(2)
因为

所以
知识点
已知函数f(x)=cos xsin 2x,下列结论中错误的是( )。
正确答案
解析
由题意知f(x)=2cos2x·sin x=2(1-sin2x)sin x.
令t=sin x,t∈[-1,1],
则g(t)=2(1-t2)t=2t-2t3.
令g′(t)=2-6t2=0,得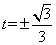
当t=±1时,函数值为0;
当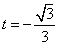
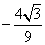
当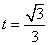
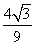
∴g(t)max=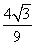
即f(x)的最大值为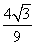
知识点
在平面直角坐标系






(1)求动点

(2)设过点








正确答案
(1)
(2)
解析
(1)解:设动点


整理得
所以动点


(2)当直线


当直线


将



设



设



所以
由题意可知
又直线

令

当


当


综上所述,点

知识点
已知函数f(x)=|x﹣2|﹣|x﹣5
(1)证明:﹣3≤f(x)≤3;
(2)求不等式f(x)≥x2﹣8x+15的解集。
正确答案
见解析
解析
(1)f(x)=|x﹣2|﹣|x﹣5|=
当2<x<5时,﹣3≤2x﹣7≤3
所以,﹣3≤f(x)≤3
(2)由(Ⅰ)可知
当x≤2时,f(x)≥x2﹣8x+15的解集为空集;
当2<x<5时,f(x)≥x2﹣8x+15的解集为{x|5﹣
当x≥5时,f(x)≥x2﹣8x+15的解集为{x|5≤x≤6}
知识点
在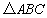
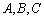
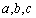
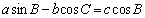
(1)判断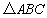
(2)若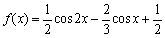
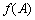
正确答案
(1)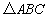
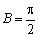
(2)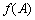
解析
(1)解:(法1)因为 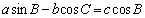
由正弦定理可得 
即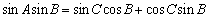
所以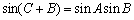
因为在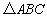
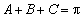
所以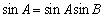
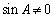
所以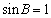
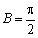
所以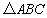
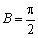
(法2)因为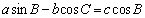
由余弦定理可得 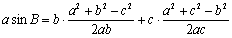
即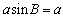
因为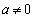
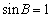
所以在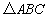
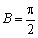
所以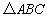
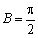
(2)解:因为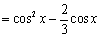
=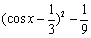
所以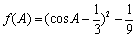
因为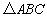
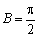
所以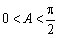
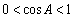
所以当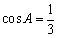
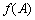
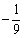
所以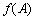
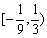
知识点
四棱锥










(1)求证:
(2)若

的余弦值;
(3)若



正确答案
见解析
解析
(1)证明:取


因为
所以
因为菱形

所以
所以
因为
所以

所以
(2)解:由(1)知
因为侧面

且平面

所以

以

则



因为


所以 

所以平面

因为 

设平面

令




由图可知,二面角

(3)解:因为

由(2)知

若设

由

在平面


所以平面

又因为

所以
即

所以,当


知识点
已知






(1)求
(2)当


正确答案
(1)
解析
(1)因为
即

所以 
(2)由
故
由


由正弦定理,

故
知识点
在△ABC中,已知A=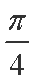

(1)求cosC的值;
(2)若BC=2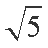
正确答案
见解析。
解析
(1)
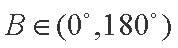
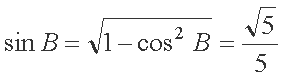
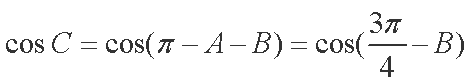
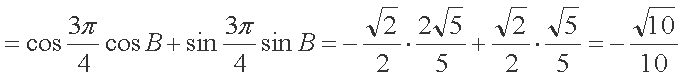
(2)由(1)可得
由正弦定理得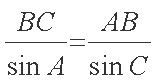
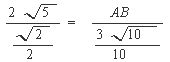
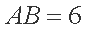
在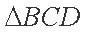

知识点

正确答案
解析



知识点
在△
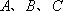
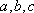
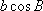
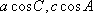
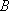
正确答案
解析
略
知识点
已知中心为O的正方形ABCD的边长为2,点M,N分别为线段BC,CD上的两个不同点,且|

正确答案
解析
如图所示,建立平面直角坐标系。
设M(2,b),N(a,2),∵

又O(1,1),∴
令a+b﹣2=t,则目标函数b=﹣a+2+t,
作出可行域

①当目标函数与圆弧相切与点P时,

②当目标函数经过点EF时,t=2+1﹣2=1取得最大值。
∴

故答案为
知识点
扫码查看完整答案与解析