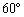- 三角函数与三角恒等变换
- 共3475题
已知函数
(1)求f(x)的最小正周期;
(2)设
正确答案
见解析。
解析
知识点
在△ABC中,已知D是AB边上一点,若

正确答案
解析
略
知识点
若


正确答案
解析


因此


知识点
在△ABC中,角A,B,C的对边分别为a,b,c,已知

(1)求B和C;
(2)若
正确答案
见解析。
解析
(1)由

∴
…………………………………(2分)
即
∴
∵
∴
∴
又

解得
(2)由(1)
得
∴△ABC的面积

知识点
已知数列


(1)求数列

(2)若对每一个正整数


①求

②记






正确答案
见解析
解析
解:(1)因为





又当n=1时,

(2)①由(1)得
(i)若



此时
(ii)若


(iii)若




此时
综上所述,


②(i)当



当


(ii)当










所以此时满足题意的最大正整数
知识点
已知函数
(1)求
(2)求函数


正确答案
(1)
(2)
解析
因为
=
=
=
(1)
=
(2)因为 
所以 
当 



当


知识点
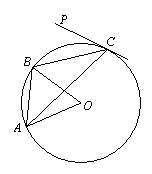
若
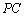
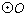
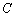
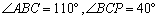
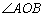
正确答案
解析
如图,弦切角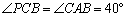
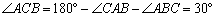
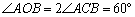
知识点
已知函数

(1)求函数
(2)若

正确答案
(1)

(2)
解析
(1)由题设
由

故函数


(2)由

考察函数

于是
故

知识点
位于A处的雷达观测站,发现其北偏东45°,与



(1)求
正确答案
(1)

解析
解析:(1)

(2)利用余弦定理
该船以匀速直线行驶了20分钟的路程为
该船的行驶速度
知识点
已知









(1)求
(2)求
正确答案
(1)2(2)
解析
解析:(1)在


即


(2)由


在

则
由于

所以
知识点
已知

(1)若

(2)若函数y=f(x)的定义域为[
正确答案
(1)
解析
(1)f(x)=-2asin2x+2asinxcosx+a+b=2asin+b,
∵a>0,∴由2kπ-≤2x+≤2kπ+得, kπ-≤x≤kπ+,k∈Z。
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z)
(2)x∈[,π]时,2x+∈[,], sin∈[-1,]
当a>0时,f(x)∈[-2a+b,a+b]
当a<0时,f(x)∈[a+b,-2a+b]
综上知,
知识点
设

(1)若


(2) 若

(3) 若

正确答案
见解析
解析
方法一在区间

(1)当



(2)①若








②若


③若


在区间


在区间


故在区间


由


故所求实数a的取值范围是
方法二、函数




令
由


在区间


在区间


故在区间


注意到




故方程


即所求实数a的取值范围是
[注:解法二只说明了

(3)设

原不等式
令


设函数
求导得:
故函数

即不等式

知识点
已知


(1)求
(2)设



正确答案
见解析
解析
(1)由正弦定理有:
∴

∴

(2)


当


又


当


此时
∴综上
知识点
在


(1)求角A的大小;
(2)若


正确答案
(1)
解析
解析:(1)在△ABC中,∵
由正弦定理有:
∴

∵



(2)解法一:由已知


由正弦定理得:



∵



故△ABC的周长l的取值范围是
解法二:周长


∴

又

即△ ABC的周长l的取值范围是
知识点
某车站每天上午安排A、B两种型号的客车运送旅客,A型车发车时刻可能是8:00,8:20,8:40;B型车发车时刻可能是9:00,9:20, 9:40,两种型号的车发车时刻是相互独立的,下表是该车站最近100天发车时刻统计频率表:
(1)直接写出表中的m,n的值;
(2)某旅客8:10到达车站乘车,根据上表反映出的客车发车规律,
(ⅰ)求该旅客能乘上A型客车的概率;
(ⅱ)求该旅客候车时间
(注:将频率视为概率)
正确答案
见解析
解析
(1)m=50,n=0。25。 …………………2分
(2)(ⅰ)设某旅客8:20,8:40乘上车事件分别为A,B,则A,B互斥。

(ⅱ)可能取值为







知识点
扫码查看完整答案与解析