三角函数与三角恒等变换_章节学习

1

题型：填空题

|

填空题 · 5 分

15.已知，且在区间有最小值，无最大值，则＝_______．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 12 分

22．已知，定义域为D．

（1）化简，并求定义域D；

（2）是否存在，使得与相等？若存在，求的值；若不存在，请说明理由．

正确答案

（1），

，

又因为，

即，

解得：定义域为且．

（2）若，则，

所以，即，

此时，，

即为存在的值．

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 5 分

12．的系数是_________（用数字作答）．

正确答案

- 5

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 18 分

22．已知函数（其中为实常数）在区间为减函数且在区间为增函数。

（1）求的解析式；

（2）若不等式在上有解，求实数的取值范围；

（3）若有三个不同的实数解，求实数的取值范围．

正确答案

（1），

令，则在区间为减函数且在区间为增函数所以在区间为减函数且在区间为增函数

由已知得

故，或由图像可得

（2）可化为，

化为，令，则，

因，故，记，因为，故，

所以的取值范围是．

（3）原方程可化为，令，则，有两个不同的实数解，，其中，，或，．

记，则 ①或 ②

解不等组①，得，而不等式组②无实数解．所以实数的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：填空题

|

填空题 · 5 分

11．已知的三内角、、所对边长分别为是、、，设向量，，若∥，则角的大小为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：填空题

|

填空题 · 5 分

14．已知在平面直角坐标系中，A（-2，0），B（1，3），O为原点，且，（其中α+β=1，α，β均为实数），若N（1， 0），则的最小值是．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 12 分

18.在中，三个内角，，的对边分别为，，，其中，且

（1）求证：是直角三角形；

（2）设圆过三点，点位于劣弧上，，用的三角函数表示三角形的面积，并求面积最大值.

正确答案

（1）证明：由正弦定理得，整理为，

即sin2A＝sin2B ∴2A＝2B或2A＋2B＝π,

即A＝B或A＋B＝∵，∴A＝B舍去.

由A＋B＝可知c＝，∴ΔABC是直角三角形

（2）由（1）及，得，

在RtΔ中，

所以，

，

因为，所以，，

当，即　时，最大值等于

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域两角和与差的正弦函数正弦定理

1

题型：填空题

|

填空题 · 4 分

11．函数的值域为（）

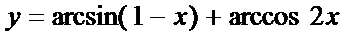
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域反函数正弦函数的定义域和值域余弦函数的定义域和值域

1

题型：简答题

|

简答题 · 18 分

22．已知函数满足关系，其中是常数

（1）设，，求的解析式；

（2）设计一个函数及一个的值，使得；

（3）分别为的三个内角对应的边长，，若，且时取得最大值，求当取得最大值时的取值范围

正确答案

（1），；

（2），

若，则

，

（3）

因为且时取得最大值，

且

因为为三角形内角，所以，所以．

由正弦定理得，，

，，

所以的取值范围为

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：填空题

|

填空题 · 4 分

12．在由数字0、1、2、3、4、5所组成的没有重复数字的四位数中任取一个数，该数能被5 整除的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：单选题

|

单选题 · 20 分

开学初，小源到建设银行营业网点兑换了此前在网上预约的中国高铁纪念币。这枚纪念币由中国人民银行发行，面额10元，每人限兑20枚，且需要提前预约。小源打算与班上同学分享自己的喜悦。他可以向大家这样介绍

①纪念币面额和实际购买力都是由中国人民银行规定的

②纪念币可以直接购买商品，也具有支付手段等货币职能

③纪念币发行量有限，具有一定的收藏价值和升值空间

④纪念币不能与同面额人民币等值流通，必须在规定时间地点使用

A①③

B①④

C②③

D②④

正确答案

C

解析

①错误，国家无权规定纪念币的实际购买力；④错误，纪念币与同面额人民币等值流通，在任何时间地点都可使用；由中国人民银行发行的纪念币属于法定货币，可以直接购买商品，也具有支付手段等货币职能，因其发行量有限，具有一定的收藏价值和升值空间，故②③正确。

知识点

生产决定消费

1

题型：简答题

|

简答题 · 12 分

19．如图，几何体中，四边形为菱形，，，面∥面,、、都垂直于面,且，为的中点，为的中点.

（Ⅰ）求证：为等腰直角三角形；

（Ⅱ）求二面角的余弦值.

正确答案

（I）

连接，交于，因为四边形为菱形，，所以

因为、都垂直于面,，

又面∥面,

所以四边形为平行四边形 ,则

因为、、都垂直于面,则

所以

所以为等腰直角三角形

（II）取的中点，因为分别为的中点，所以∥

以分别为轴建立坐标系，

则

所以

设面的法向量为，

则，即且

令，则

设面的法向量为，

则即且

令，则

则,则二面角的余弦值为

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 14 分

22．设函数f （θ）＝sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．

（1）若点P的坐标为（），求f（θ）的值；

（2）若点P（x，y）为平面区域，上的一个动点，试确定角θ的取值范围，并求函数f（θ）的最小值和最大值．

正确答案

（1）由点P的坐标和三角函数的定义可得

sinθ＝，cosθ＝．

于是f（θ）＝sinθ＋cos θ＝＝2．

（2）作出平面区域Ω（即三角区域ABC），

其中A（1，0），B（1，1），C（0，1）．

于是0≤θ≤．

又f（θ）＝sinθ＋cosθ＝2sin（θ＋），

且≤θ＋≤，

故当θ＋＝，即θ＝时，

f（θ）取得最大值，且最大值等于2 ；

当θ＋＝，即θ＝0时，

f（θ）取得最小值，且最小值等于1．

解析

解析已在路上飞奔，马上就到！

知识点

任意角的三角函数的定义正弦函数的定义域和值域两角和与差的正弦函数

1

题型：填空题

|

填空题 · 4 分

10．的___________条件。

正确答案

既不充分也不必要

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

1

题型：单选题

|

单选题 · 5 分

8．设随机变量服从标准正态分布，已知，则（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点