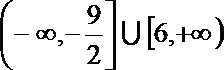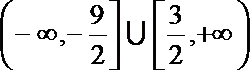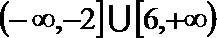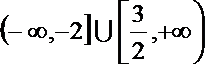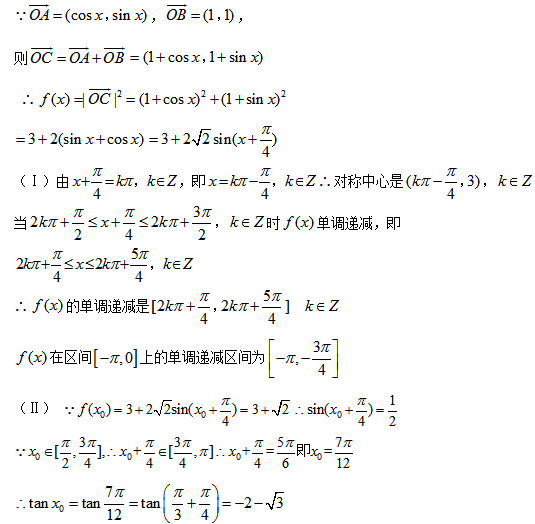- 三角函数与三角恒等变换
- 共3475题
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数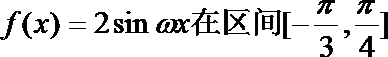
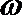
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.关于函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若关于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求f(x)的最小正周期和值域;
(2)若x=x0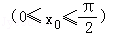
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知a=(sinx,-cosx),b=(cosx,

(1)求f(x)的最小正周期,并求其图像对称中心的坐标;
(2)当0≤x≤
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在直角坐标系中,已知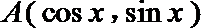
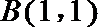
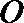
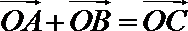
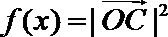
(Ⅰ)求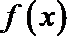
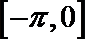
(Ⅱ)若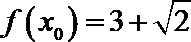
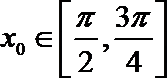
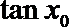
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.△ABC的三个内角以弧度度量,设M=Acos B+sin Acos C,则( ).
正确答案
解析
(1)△ABC为锐角三角形时,M>0.
(2)△ABC为直角三角形时,M>0.
(3)△ABC为钝角三角形时,①若A>
②若B>
③若C>
由于A>sin A,因此M>0.
由(1)、(2)、(3)知答案为A.
知识点
20.把函




(1)求a的最小值;
(2)当a取最小值,求函数

正确答案
(1)
∴

∴


(2)由(1)知
即
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数









正确答案
解析
因为




知识点
12.已知边长为6的正三角形



则
正确答案
3
解析
设



又B、P、E三点共线,






考查方向
解题思路
本题主要考查向量的线性运算,向量的数量积,向量的坐标运算。
解题步骤如下:由向量基本定理和B、P、E三点共线求出向量 

易错点
本题不容易想到利用B、P、E三点共线寻找突破口,不能正确运用向量的基本定理解决问题。
知识点
9.如图是某一几何体的三视图,则该几何体的体积是()
正确答案
解析
先计算出长方体的体积V=1×1×2=2其一半为所求几何体的体积即为1。
故选B
考查方向
解题思路
1、先在长方体中切割出原几何体。
2、进行补形再计算其几何体体积,其一半为几何体的体积。
易错点
1、本题易忽视左视图中的虚线而还原几何体时出错。
2、本题在几何体体积计算上不进行补形而计算出错。
知识点
17. 在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)求
(Ⅱ) 若角A是钝角,且c=3,求b的取值范围.
正确答案
(1)2;(2)
解析
试题分析:本题属于三角形中的正弦定理、余弦定理应用问题,题目的难度适中。(1)求解时一定要定位好是角化边还是边化角;(2)在求边的范围时切记不要忘记三角形中三边关系。
(1)由正弦定理
(2) 由余弦定理


由①②得
考查方向
解题思路
本题考查了正弦定理、余弦定理应用,解题步骤如下:1、分析判断后边化角,利用和角公式整理后再利用角化边。2、由余弦定理解出
易错点
1、第一问边角转化判断失误而错解。2、第二问没想到用三边关系缩小范围而出错。
知识点
扫码查看完整答案与解析