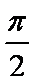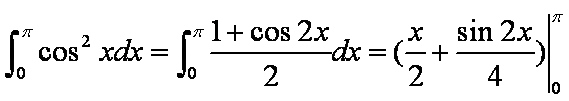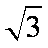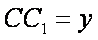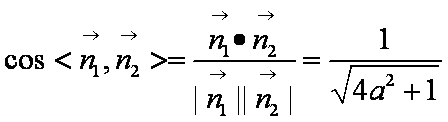- 三角函数与三角恒等变换
- 共3475题
计算: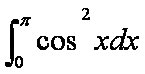
正确答案
解析
由定积分的定义得

知识点
函数
正确答案
解析
原函数的图象是由

知识点
已知椭圆


(1)求椭圆
(2)直线




正确答案
(1)
解析
解析:(1)解法1:由抛物线方程,得焦点

故
又椭圆


由①②消去



从而

解法2:由抛物线方程,得焦点
故椭圆的方程为
(2)

所以,

由
显然





由抛物线的定义,得
综上,当直线l垂直于


知识点
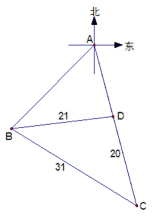
在城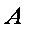
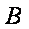
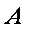
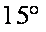
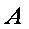
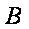
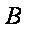
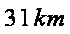
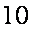
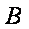
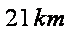
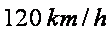
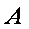
正确答案
见解析
解析
如图,由题意知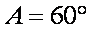
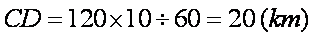
则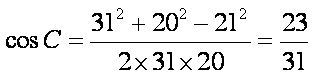
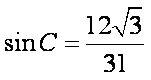
故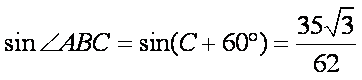
在△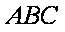
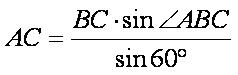
带入已知数据可求得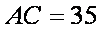
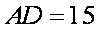
所以,汽车要到达城
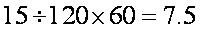
知识点
已知




正确答案
解析
由二项式定理知: 





知识点
在直角坐标系x Oy中,直线 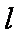
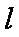
正确答案
解析
由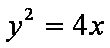
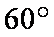
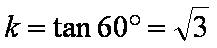
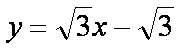
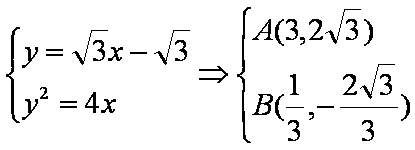
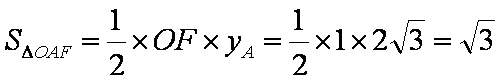
知识点
已知

(1)当

(2)在



正确答案
见解析
解析
∵

由


(1)由

∴当
(2)由


而


在


∴
∴

∵

知识点
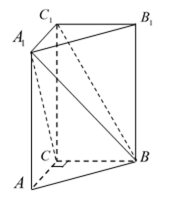
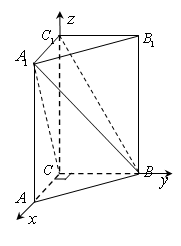
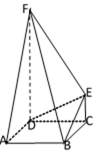
如图,在直三棱柱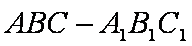
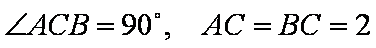
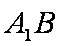
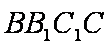
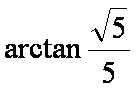
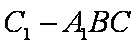
正确答案
见解析
解析
法一: 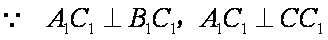
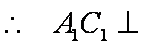
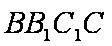
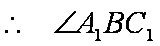
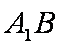
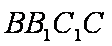
设
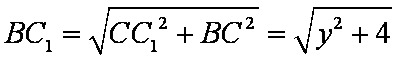
所以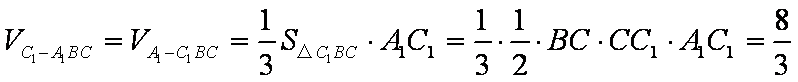
法二:如图,建立空间直角坐标系,设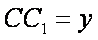
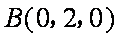
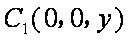
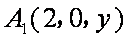
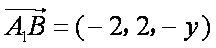
平面
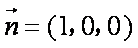
设直线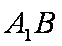
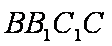
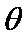
则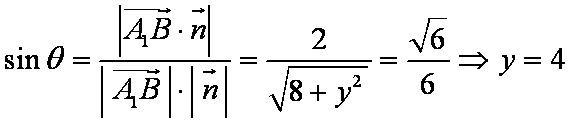
所以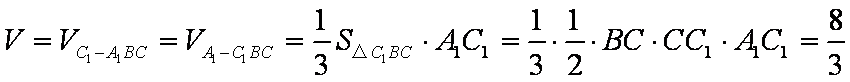
知识点
在三角形ABC中,若角A、B、C所对的三边a、b、c成等差数列,则下列结论中正确的是____________。
①b2≥ac;
②
③
④
正确答案
①③④
解析
由a、b、c成等差数列,则
∴
∴
由正弦定理得:
又由余弦定理得:



∴
知识点
O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足
正确答案
解析


知识点
如图所示,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB = 7, C是圆上一点使得BC = 5,
正确答案
解析
∵

∴


知识点
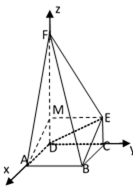
如图,FD垂直于矩形ABCD所在平面,CE//DF,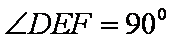
(1)求证:BE//平面ADF;
(2)若矩形ABCD的一个边AB =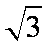
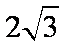
正确答案
见解析
解析
解(1)法1:过点E作CD的平行线交DF于点M,连接AM。
因为CE//DF,所以四边形CEMD是平行四边形,可得EM = CD且EM //CD,于是四边形BEMA也是平行四边形,所以有BE//AM,而直线BE在平面ADF外,所以BE//平面ADF,
法2:以直线DA为x轴,直线DC为y轴,直线DF为z轴,建立空间直角坐标系,则平面ADF的一个法向量为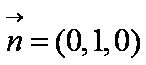
设AB = a,BC = b,CE = c,则点B、E的坐标分别为(b,a,0)和(0,a,c),那么向量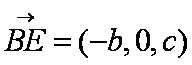
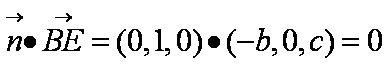
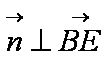
(2)由EF =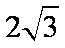
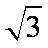
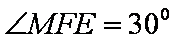
由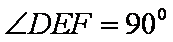
设BC = a,则点B的坐标为(a,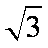
又点E、F的坐标分别为(0,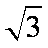
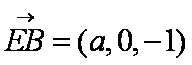
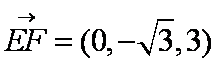
设平面BEF的一个法向量为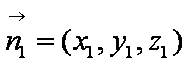
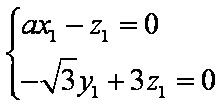
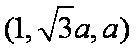
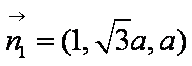
易知平面DEF的一个法向量为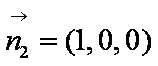
由于此时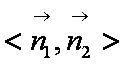

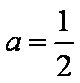
所以另一边BC的长为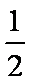
知识点
如图,在杨辉三角中,斜线l上方,从1开始箭头所示的数组成一个锯齿数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于____________.
正确答案
283
解析
由条件知道:该数列的奇数项分别为1,3,6,10,15,21,28,36,45,55,…,偶数项分别为3,4,5,6,7,8,9,10,11,…,把奇数项的前10项与偶数项的前9项相加即得S19=283.
知识点
已知




则
正确答案
4
解析



知识点
已知ai>0(i=1,2,…,n),考查
①
②
③
归纳出对a1,a2,…,an都成立的类似不等式,并用数学归纳法加以证明。
正确答案
见解析。
解析
结论:(a1+a2+…+an)(


证明:①当n=1时,显然成立;…………………………(6分)
②假设当n=k时,不等式成立,
即:(a1+a2+…+ak)(


那么,当n=k+1时,
(a1+a2+…+ak+ak+1)(



=(a1+a2+…+ak)(






≥k2+(





≥k2+2k+1
=(k+1)2
即n=k+1时,不等式也成立,…(12分)
由①②知,不等式对任意正整数n成立,…(13分)
知识点
扫码查看完整答案与解析