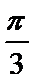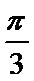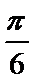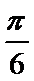- 三角函数与三角恒等变换
- 共3475题
12.已知函数






正确答案
知识点
若将函数y=2sin 2x的图像向左平移个单位长度,则评议后图象的对称轴为
正确答案
知识点
为了得到函数

正确答案
知识点
某同学用“五点法”画函数
时,列表并填入了部分数据,如下表:
18.请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
析式;
19.将




正确答案
(Ⅰ)根据表中已知数据,解得
且函数表达式为
解析
(Ⅰ)根据表中已知数据可得:



且函数表达式为
考查方向
解题思路
(Ⅰ)根据已知表格中的数据可得方程组

易错点
出现粗心的错误。
正确答案
离原点

解析
由(Ⅰ)知












考查方向
解题思路
由(Ⅰ)并结合函数图像平移的性质可得,函数

易错点
平移出错。
4.要得到函数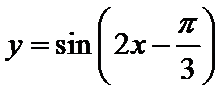
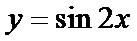
正确答案
解析
∵
∴只要将函数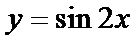
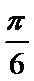
∴所以选项D为正确选项
考查方向
解题思路
先将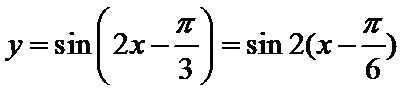
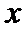
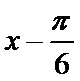
易错点
本题易在相位变换对变量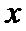
知识点
9.已知函数


正确答案
解析
根据平移后与原函数重合可知平移的距离为周期可知

考查方向
解题思路
该题解题思路
1)根据平移后与原函数重合可知平移的距离为周期的整数倍
2)使用周期与
3)利用解析式求最值得到结果
易错点
主要易错于无法理解与原图重合对应的含义
知识点
6.要得到y=sin2x-
正确答案
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难。注意化简时对φ的选取.
考查方向
本题主要考查了三角函数的图象与性质,在近几年的各省高考题出现的频率非常高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
本题考查三角函数的图象与性质,解题步骤如下:
由题可知,函数解析式化简为y=2sin(2x-


易错点
本题易在公式化简上发生错误。
知识点
9.已知函数





正确答案
解析










考查方向
函数图象的平移,函数的奇偶性
解题思路
先求出平移后的函数,然后根据奇函数的定义化简求参数,最后利用三角函数周期的特点判断最小正周期。
易错点
函数平移概念理解不透彻
知识点
18.如图,

















正确答案
(1)在△ABC中,
由余弦定理可知:
∴

又∵

(2)T=2×(10+5)=30,
∴
∵



解析
已知两边一角,三角形可解。利用余弦定理OC.进而确定三角函数式的表达式,得到周期和坐标
考查方向
三角形的面积,余弦定理,三角函数的解析式.
解题思路
先解三角形,然后确定三角函数表达式,进而求周期
易错点
解三角形,余弦定理求解错误
知识点
2.已知函数



正确答案
解析
由题可知:y=sin[w(x-




考查方向
本题主要考查三角函数的图像变换
解题思路
1、求出变换后的函数解析式;
2、表示对称性,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示图像变换时发生错误。
知识点
9.函数




正确答案
解析
因为

又因为其图像关于Y轴对称,所以有,
所以函数在
带入数字可得,最大值为
考查方向
三角函数的图像的平移与变换
解题思路
先求出图像向右移动后的函数解析式,然后根据其与y轴对称,求出参数角的大小,进而求出所在区间的最大值
易错点
平移变换错误,计算错误
教师点评
此类题要充分掌握函数图象变换的性质和特点
知识点
6.已知函数




正确答案
解析
第一步y=cosx变换成
然后变成
所以对称轴方程为
即
所以选D
考查方向
三角函数图像的伸缩变换
解题思路
按照题意,按步骤变换函数图象,然后再判断对称轴
易错点
对三角函数图象变换掌握不好
知识点
9.若将函数


正确答案
解析
由

又所得图象关于y轴对称,则
∴当k=-1时,

故选C.
考查方向
解题思路
把函数式



易错点
三角函数图象的平移应遵循“左加右减”的原则.
知识点
11.将函数

正确答案
解析
将函数


故选B.
考查方向
解题思路
根据左加右减的原则进行变换即可.
易错点
图像的平移变换,伸缩变换因先后顺序不同平移的量不同,



知识点
17.某同学用“五点法”画函数
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
(2)将





正确答案
(1)根据表中已知数据,解得
且函数表达式为
(2)由(1)知 

因为


令


由于函数


解得





解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析