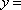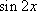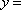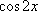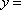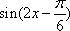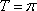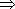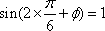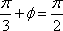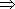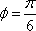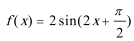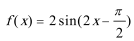- 三角函数与三角恒等变换
- 共3475题
函数


正确答案
解析
略
知识点
函数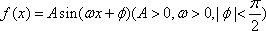
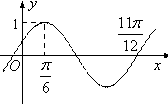
如图示,则将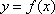
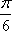
图象解析式为 ( )
正确答案
解析
由图像知A=1, 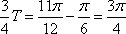
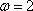
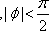
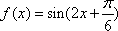
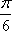
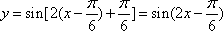
知识点
如图是函数

正确答案
解析
由图知
将点
故选 C
知识点
已知函数
(1)求函数
(2)若

正确答案
见解析。
解析
解:(1)易得






(2)





知识点
已知函数






(1)求
(2)若

正确答案
见解析。
解析
(1)


所以
(2)
由



则

从而

知识点
已知函数 

(1)若 
(2)将函数 





正确答案
见解析。
解析
知识点
5.已知函数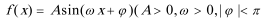
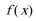
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 函数



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
3.函数周期为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:函数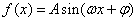
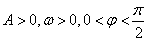

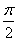
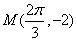
(1)求:
(2)当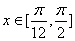
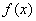
正确答案
(1)由最低点为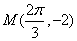

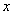
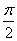
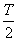
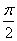
即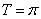
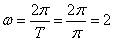
由点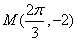
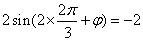
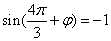
∵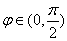
∴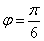
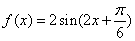
(2)∵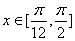
∴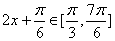
当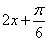
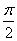
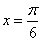

当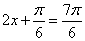
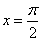
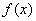
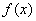
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数




(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<)的图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( )
正确答案
解析
由图象可知A=1,T=π,∴ω=














知识点
16.某同学用“五点法”画函数
(1)请写出上表的


(2)将







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设偶函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析