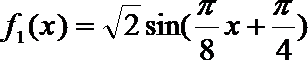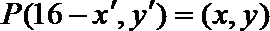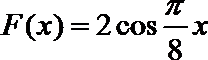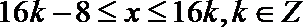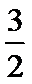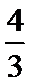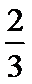- 三角函数与三角恒等变换
- 共3475题
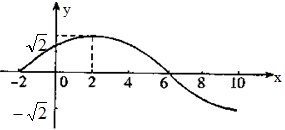
7. 已知函数
如右图所示,如果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.
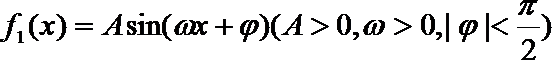
(1)求此函数的解析式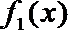

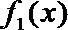
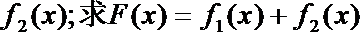
正确答案
(1)
(2)设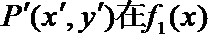
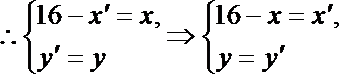
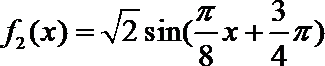
单增区间
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


(1)求函数
(2)已知横坐标分别为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数


(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( ).
正确答案
解析
根据题意过点P作PE







知识点
1.已知ω>0,|φ|<


正确答案
解析
由图可知,




∴f(x)=sin(2x+φ),又
∴φ=2kπ+


∴f(x)=sin(2x+
令x=0,得M(0,



∴












知识点
4. 函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是( )
正确答案
考查方向
本题主要考查了由三角函数的图象和性质求解析式,在近几年的各省高考题出现的频率较高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
1、由图可知

2、把点



易错点
1、本题易在对性质理解不到位没有办法求出
2、本题在求

知识点
9.己知A(x1,0),B(x2,1)在函数f(x)=2sin(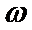
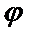
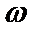
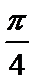
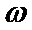
正确答案
解析
将点A,B代入f(x)表达式,得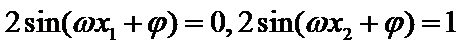
解得: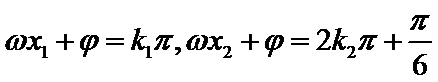
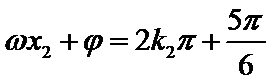
两式相减得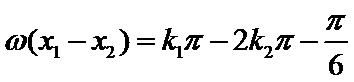
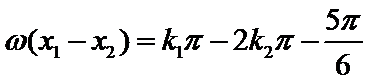
因此当|x1-x2|的最小值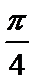
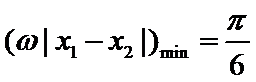
所以
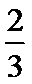
考查方向
解题思路
把点A,B代入函数表达式,然后求出|x1-x2|的关系式,然后研究其最小值即可。
易错点
不能正确理解题意。
知识点
扫码查看完整答案与解析