- 三角函数与三角恒等变换
- 共3475题
15.设函数
(1)求函数
(2)当

正确答案
(1)
(2)
解析
试题分析:本题属于三角函数图像的基本问题,题目的难度是逐渐由易到难,(1)直接按照求A、ω、φ步骤来求(2)转化成求函数的最值,要结合图像,要特别注意函数的定义域。
(1)由图象知,
又



所以


即


所以
(2)当

所以

考查方向
解题思路
本题考查三角函数的图形和性质,解题步骤如下:
1、根据函数图像,确定A、ω、φ,进而求出函数
2、求函数
易错点
1、第一问中的根据角的范围如何确定φ。
2、第二问中求
知识点
已知函数
17.求函数
18.在




正确答案
解析
(1)由图象知A=1, 
将点


所以
考查方向
解题思路
利用函数的图象,求出A,通过函数的周期求出ω,通过函数的图象经过


易错点
三角函数的解析式中,求的值是难点,熟悉正余弦函数图象是关键.
正确答案
解析
由
所以
因为

所以

所以
考查方向
解题思路
利用

易错点
无
已知函数
17.求函数
18.在




正确答案
解析
(1)由图象知A=1, 
将点


所以
考查方向
解题思路
利用函数的图象,求出A,通过函数的周期求出ω,通过函数的图象经过


易错点
三角函数的解析式中,求的值是难点,熟悉正余弦函数图象是关键.
正确答案
解析
由
所以
因为

所以

所以
考查方向
解题思路
利用

易错点
无
7.先将函数

正确答案
解析
向右平移



考查方向
解题思路
先向右平移


注意本题的答案还可以继续利用诱导公式进行变形,若我们在做出来的答案没有与之相同的选项的时候,就需要进一步变形。
易错点
1、左右平移的时候没有乘
2、图像关于
知识点
8.函数
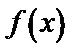
正确答案
解析
由图可知,
故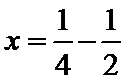
即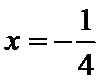
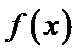
又因为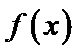
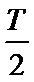
所以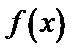
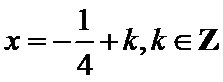
应选C.
考查方向
本题主要考查三角函数的图象,对称轴,周期等内容,难度不大,考查数形结合的思想方法。
解题思路
1.结合图形算出周期;
2.利用周期与对称轴之间的距离关系,得出结果,
应选C。
易错点
本题不易理解周期与对称轴之间,以及对称轴与对称轴之间的距离关系。
知识点
已知


正确答案
解析
【解析1】因为






【解析2】


知识点
17.在公比为




(Ⅰ)求
(Ⅱ)若函数








正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题属于数列和三角函数中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意图像的应用.
(Ⅰ) 解:由题可知

故
(Ⅱ)∵点

∴
又∵
如图,连接

又∵
∴
∴
考查方向
本题考查了数列与三角函数的知识,涉及到等比数列及三角函数的应用,是高考题中的高频考点.
解题思路
本题考查数列与三角函数的知识,解题步骤如下:
1、利用通项公式求解。
2、利用函数图像性质代入求解。
易错点
三角函数图像易错。
知识点
13.已知函数





正确答案
解析
由题意可知
又∵函数为偶函数 ∴
又∵
考查方向
解题思路
根据正弦型函数的图像容易得到




易错点
本题易于在求解
知识点
8.已知




正确答案
解析
三角函数相邻两对称轴正好跨度了半个周期所以



又

考查方向
解题思路
利用堆成轴间距求出周期确定
易错点
无法利用条件确定周期进而求解
知识点
3.如图,某港口一天6时到18时的水深变化曲线近似满足函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知









(1)求
(2)求
正确答案
(1)2(2)
解析
解析:(1)在


即


(2)由


在

则
由于

所以
知识点
已知函数
(1)求
(2)在




的形状。
正确答案
见解析。
解析
(1)


所以

﹙2﹚由

所以
因为


由余弦定理


所以

所以
知识点
已知


正确答案
解析
解析一:

解析二:

知识点
9. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知
(1)求
(2)求
正确答案

(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析