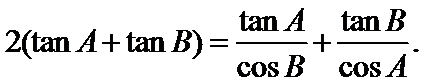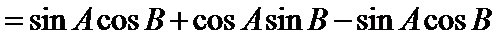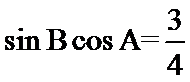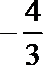- 三角函数与三角恒等变换
- 共3475题
16.(本小题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)证明:a+b=2c;
(Ⅱ)求cosC的最小值.
正确答案
知识点
设△ABC的内角A,B,C的对边分别为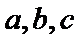
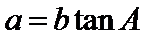
18.证明:
19.若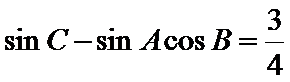
正确答案
由
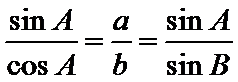
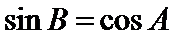
解析
见答案
考查方向
解题思路
由题及正弦定理得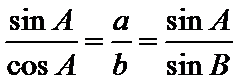
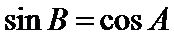
易错点
不会想到切割化弦;
正确答案
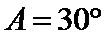
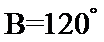
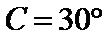
解析
因为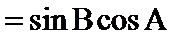
由(1)知
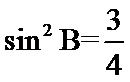
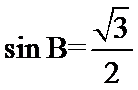
故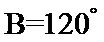
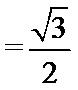
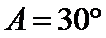
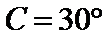
综上所述,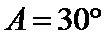
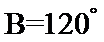
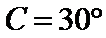
考查方向
解题思路
由两角和与差的公式化简得
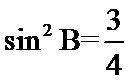
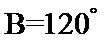
易错点
做第(2)问时联系不上第(1)问的结论。
已知α为锐角,cos(α+

15.求tan(α+
16.求sin(2α+
正确答案
(1)2 ;
解析
解:(1)因为α∈(0,



所以sin(α+


所以tan(α+

考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
正确答案
(2)
解析
解:
(2)因为sin(2α+




cos(2α+



所以sin(2α+







考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
14.在



则
正确答案
解析
因为


所以

考查方向
解题思路
先根据余弦定理表示出
易错点
利用定理进行恒等变换时错误
知识点
化简sin2013°的结果是( )
正确答案
解析
sin2013°=sin(360°×5+213°)=sin213°=sin(180°+33°)=﹣sin33°。
故选C
知识点
已知









(1)求
(2)求
正确答案
(1)2(2)
解析
解析:(1)在


即


(2)由


在

则
由于

所以
知识点
已知函数
(1)求
(2)在




的形状。
正确答案
见解析。
解析
(1)


所以

﹙2﹚由

所以
因为


由余弦定理


所以

所以
知识点
已知


正确答案
解析
【解析1】因为






【解析2】


知识点
已知


正确答案
解析
解析一:

解析二:

知识点
19.已知
(1)求
(2)求
正确答案

(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
4.若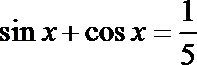
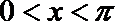
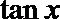
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知sin2θ(1+ctgθ)+cos2θ(1+tgθ)=2, 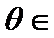
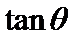
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC中,a,b,c分别是角A,B,C的对边,若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析