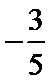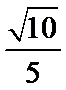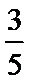- 三角函数与三角恒等变换
- 共3475题
13.
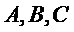





正确答案
解析
试题分析:因为




所以
考查方向
解题思路
先根据


易错点
相关知识点不熟悉导致出错。
教师点评
三角函数和差公式,正弦定理.
知识点
已知α为锐角,cos(α+

15.求tan(α+
16.求sin(2α+
正确答案
(1)2 ;
解析
解:(1)因为α∈(0,



所以sin(α+


所以tan(α+

考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
正确答案
(2)
解析
解:
(2)因为sin(2α+




cos(2α+



所以sin(2α+







考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
9.若

正确答案
解析
由已知,
=
考查方向
解题思路
三角恒等变换的主要题目类型是求值,在求值时只要根据求解目标的需要,结合已知条件选用合适的公式计算即可.本例应用两角和与差的正弦(余弦)公式化解所求式子,利用同角关系式使得已知条件可代入后再化简.
易错点
求解过程中注意公式的顺用和逆用
知识点
3. 已知


正确答案
解析




所以

考查方向
解题思路
1.先根据题中条件求出角
易错点
1.利用诱导公式在化简时出错;2.对于特殊角的三角函数值记忆出错。
知识点
6.已知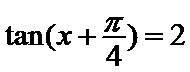
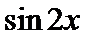
正确答案
解析
由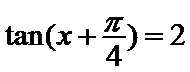
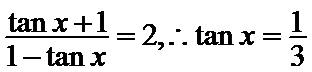
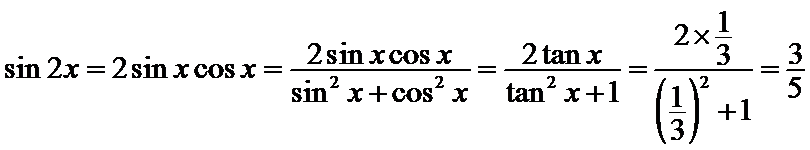
考查方向
解题思路
1.先利用两角和的正切公式求出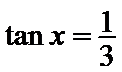
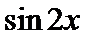
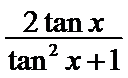
易错点
1. 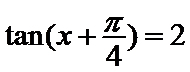
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数
正确答案
解析


=

当


知识点
7.若


正确答案
解析

联立可得
考查方向
三角函数
解题思路
三角恒等变换得到
由a所在象限再进行计算。
易错点
不注意角的象限
教师点评
本题难度中等,要求学生能够熟练应用三角函数化简与恒等变换和计算。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数
(1) 当m=0时,求

(2) 当

正确答案
(1)
(2)m=-2
解析
(1)当m=0时,


从而得:
(2)
化简得:
当


代入上式,m=-2.
知识点
已知函数
(1)求函数

(2)若

正确答案
见解析。
解析
(1)解:由
所以函数
因为





(2)解:由(1)可知
又因为
由
从而
所以
知识点
函数
正确答案
解析
f(x)=sinx-cos(x+





知识点
已知函数


(1)求
(2) 设



正确答案
(1)
(2)
解析
(1)由
(2)由(1)知






所以
知识点
扫码查看完整答案与解析