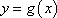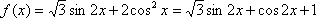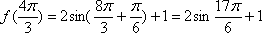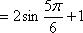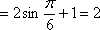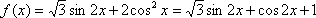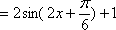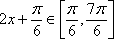- 三角函数与三角恒等变换
- 共3475题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
为了得到函数

正确答案
解析

而
由
故只需将

知识点
在

sinB=
(1)求tanC的值;
(2)若a=

正确答案
(1) 

解析
本题主要考察三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点。
(1)∵cosA=

又
=

整理得:tanC=
(2)由图辅助三角形知:sinC=
又由正弦定理知:
故
对角A运用余弦定理:cosA=
解(1) (2)得:

∴

知识点
若


正确答案
解析
因为


所以
知识点
“


正确答案
解析
当





知识点
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知
(1)求角C的大小;
(2)若
正确答案
(1)
解析
(1)由题得
即
由


即
(2)



由



所以,△ABC的面积为
知识点
已知函数

(1)求
(2)在









正确答案
见解析。
解析
(1)由题意可得





(2)


由(1)知



又

知识点
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
a.sin213°+cos217°﹣sin13°cos17°
b.sin215°+cos215°﹣sin15°cos15°
c.sin218°+cos212°﹣sin18°cos12°
d.sin2(﹣18°)+cos248°﹣sin2(﹣18°)cos48°
e.sin2(﹣25°)+cos255°﹣sin2(﹣25°)cos55°
(1)试从上述五个式子中选择一个,求出这个常数
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论。
正确答案
见解析
解析
(1)选择b,计算如下:
sin215°+cos215°﹣sin15°cos15°=1﹣


(2)根据(1)的计算结果,将该同学的发现推广,得到三角恒等式sin2α+cos2(30°﹣α)﹣sinαcos(30°﹣α)=
证明:(方法一)sin2α+cos2(30°﹣α)﹣sinαcos(30°﹣α)=sin2α+
=sin2α+







(方法二)sin2α+cos2(30°﹣α)﹣sinαcos(30°﹣α)=

=1﹣



=1﹣








知识点
将函数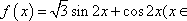
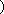
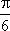
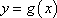
正确答案
解析
略
知识点
已知函数
(1)求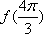
(2)当

正确答案
见解析。
解析
(1)
(2)
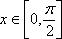
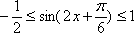
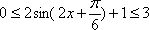
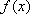
知识点
已知复数
(1)求
(2)设





正确答案
(1)
解析
(1)∵
∴

∴当


(2)∵
∴
∴
将函数

把函数


∴
知识点
若向量


正确答案
解析
略
知识点
已知函数

(1)求

(2)求函数

正确答案
(1)1;
(2)
解析

(1)
显然,函数

(2)令


又因为

函数


知识点
设函数

(1)若


(2)若




正确答案
见解析。
解析
(1)
当

而


此时



∴


(2)依题意


整理,得
又


而





知识点
设





(1)求实数

(2)
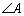




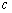



正确答案
见解析。
解析
(1)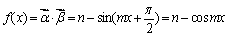
因为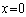
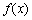
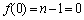
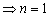
易知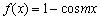

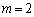

(2)由(Ⅰ)可知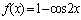
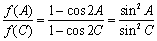
由正弦定理及余弦定理有: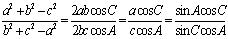
故
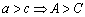
于是
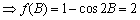
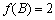
知识点
扫码查看完整答案与解析