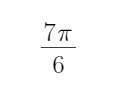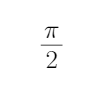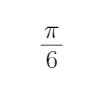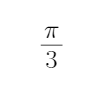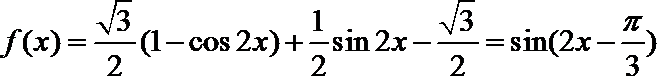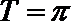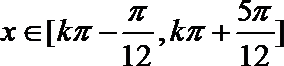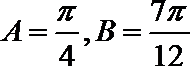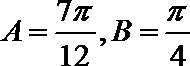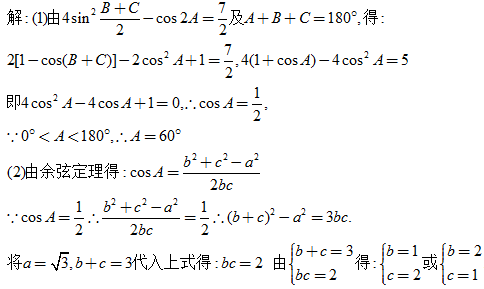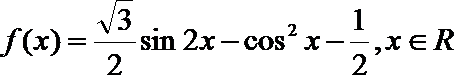- 三角函数与三角恒等变换
- 共3475题
17.已知a=(sinx,-cosx),

(1)求f(x)的最小正周期;
(2)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.将函数y=sinx-cosx的图象沿x轴向右平移a(a>0)个单位长度,所得函数的图象关于y轴对称,则a的最小值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14-15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,已知圆



15.(几何证明选讲选做题))
如图所示, 过⊙











正确答案
14. 10
15.
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数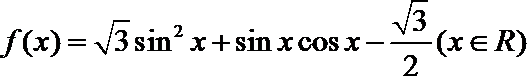
(1)求函数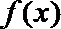
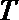
(2)在△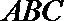
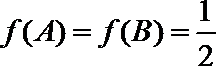
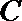
正确答案
(1)
所以周期
由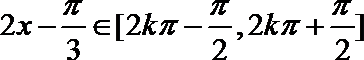
得
即函数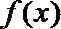
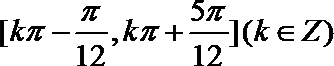
(2)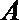
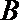
所以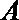
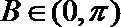
由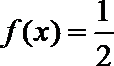
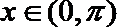
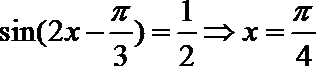
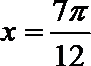
又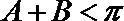
所以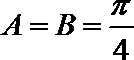
或
所以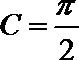
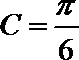
解析
解析已在路上飞奔,马上就到!
知识点
17、在△ABC中,a、b、c分别为角A、B、C的对边, 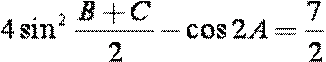
(1)求角A的度数;
(2)若a=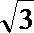
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)求
(3)当

正确答案
(1)
令
∴

(2)
故

(3) 






解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)在








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. “a=1”是函数y=cos2ax-sin2ax的最小正周期为“π”的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数
(1)求


(2)已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求函数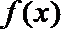
(2)确定函数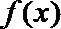
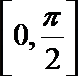
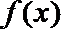
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求函数

(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17.在


(I) 求
(II)求
正确答案
(Ⅰ)解:在△ABC中,根据正弦定理,
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=
于是 sinA=

所以 sin(2A-


解析
解析已在路上飞奔,马上就到!
知识点
18.
已知向量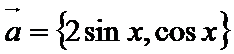

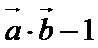
(1)求函数f(x)的最小正周期。
(2)x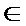
正确答案
f(x)=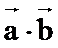
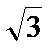
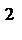
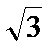
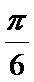
(1)T=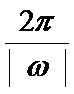
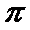
(2)f(x)=2sin(2x+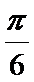
∴当2x+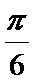
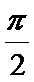
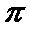
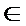
即x=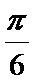

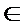
∴当x=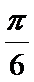
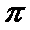
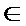
解析
解析已在路上飞奔,马上就到!
知识点
2.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析