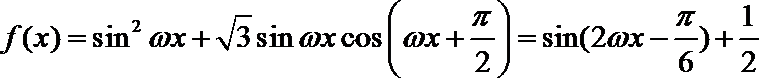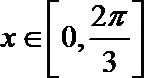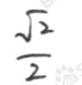- 三角函数与三角恒等变换
- 共3475题
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
17. 在







(1)求证:
(2)若


正确答案
(1)略;
(2)b=4.
解析
试题分析:本题属于解三角形中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意正弦定理的应用.
解:(1)由条件:
由于:
所以:
即:
(2)
所以:

又:
由

所以:
考查方向
本题考查了解三角形的知识,涉及到正弦定理及倍角公式的应用,是高考题中的高频考点
易错点
正弦定理求面积时容易代成cosB。
知识点
16.已知函数


(I)求
(II)在




正确答案
解:(Ⅰ)因为

所以

解
得:
所以函数
(Ⅱ) 因为
得
因为

所以

所以
根据正弦函数的图象可以看出,

此时

所以
解析
见答案
考查方向
本题主要考查正弦定理和余弦定理的性质,属于基础题
解题思路
根据题意换成三角函数一般形式,然后根据函数最值判断,第二问求出ABC角度的大小进而判定三角形形状。
易错点
混淆两个定理的性质
知识点
6.要得到y=sin2x-
正确答案
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难。注意化简时对φ的选取.
考查方向
本题主要考查了三角函数的图象与性质,在近几年的各省高考题出现的频率非常高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
本题考查三角函数的图象与性质,解题步骤如下:
由题可知,函数解析式化简为y=2sin(2x-


易错点
本题易在公式化简上发生错误。
知识点
9.化简:4sin40°-tan40°等于( )
正确答案
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难。注意化简时对两角和差公式的选取.
考查方向
本题主要考查了三角函数的公式化简计算,在近几年的各省高考题出现的频率较高,常与三角恒等变形公式等知识点交汇命题。
解题思路
本题考查三角函数的公式化简计算,解题步骤如下:
由题可知,函数解析式化简为(2sin80°-sin40°)/cos40°=[2cos(40°-30°)-sin40°]/cos40°=

易错点
本题易在公式化简上发生错误。
知识点
15.已知函数

(Ⅰ)求
(Ⅱ)设


正确答案
(Ⅰ)



解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(Ⅰ)解:

所以函数

由

得
所以函数


(注:或者写成单调递增区间为

(Ⅱ)解:由题意,得
因为函数

所以

所以

解得

又因为
所以

考查方向
本题主要考查了三角恒等变换以及三角函数的图象与性质,三角函数的性质的考查主要分以下几类:
1.三角函数的定义域,
2.三角函数的单调性与最值,
3.三角函数的周期性,
4.三角函数的奇偶性或对称性.
解题思路
本题考查三角恒等变换、三角函数的图象与性质,解题步骤如下:1.利用二倍角公式和配角公式将函数




易错点
1、第一问中的单调递增区间易错误写成集合的形式,或丢掉“
2、第二问中易利用

知识点
16.已知函数

(Ⅰ)求函数
(Ⅱ)若

正确答案
(Ⅰ)函数
(Ⅱ)

解析
本题第二问特别要注意:一定要结合函数的定义域正确书写增区间.

所以函数

(Ⅱ)解:由

得
所以函数


所以当



(注:或者写成增区间为

考查方向
解题思路
本题主要考查正、余弦的二倍角公式及
1、把

2、由

3、最后通过
易错点
本题体现了三角函数部分的基本的解题思想方法,为学生非常熟悉的题型对于第二问可能由于思维定势审题不全忽略

知识点
17.在

(1)求
(2)若


正确答案
(1)
(2)
解析
(1)由正弦定理知
即
(2)在

即


此时
考查方向
本题主要考查利用正(余)弦定理解三角形及其常用的三角恒等变换。
解题思路
(1)三角函数切化弦。
(2)第二问利用余弦定理结合基本不等式求解即可。
易错点
(1)三角公式不熟悉。
(2)第二问不会用基本不等式处理。
知识点
4.已知函数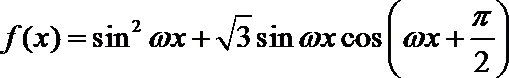
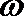

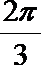
正确答案
解析
∵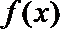
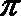
∴
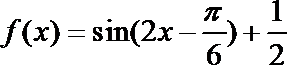
∵
∴

所以答案选A
考查方向
本题主要考查了三角函数的周期和值域
解题思路
利用利用辅助角公式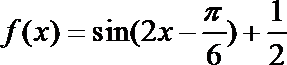
易错点
利用辅助角公式化简函数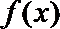
知识点
7.函数f(x)=(

正确答案
知识点
11.cos2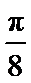
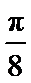
正确答案
知识点
5.设函数

正确答案
知识点
(本小题满分13分)
已知函数

(Ⅰ)若


(Ⅱ)若



正确答案
考查方向
易错点
1、本题在第一问
知识点
17.设函数
(1)求函数
(2)若





正确答案
(1)


(2)

解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关三角函数的知识,即可解决本题,解析如下:
试题解析:(1)
∴函数f(x)的最小正周期
当

当

(2)因为

∴


∵
由余弦定理得:
∴
考查方向
解题思路
(1)先用两角和与差的正弦化简
(2)先根据解析式求得角


易错点
相关知识点不熟容易证错。
知识点
扫码查看完整答案与解析