三角函数与三角恒等变换_章节学习

1

题型：单选题

|

单选题 · 5 分

5.若，则

A

B

C1

D

正确答案

A

知识点

三角函数中的恒等变换应用

1

题型：单选题

|

单选题 · 5 分

5.设函数，则的最小正周期( )

A与b有关，且与c有关

B与b有关，但与c无关

C与b无关，且与c无关

D与b无关，但与c有关

正确答案

B

解析

当，最小正周期明显是，当，首先是周期，只要判断是否是周期就可以了，

取，，，那么不是周期。说明对周期有影响。

考查方向

三角函数的周期及最小正周期的理解。

解题思路

明显常数C不会对周期产生影响，只要判断对周期的影响就可以了。

易错点

对函数最小正周期的理解偏差导致错误，可能会选C

知识点

三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 4 分

9．已知的三边长为，则该三角形的外接圆半径等于__________．

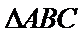
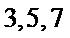
正确答案

解析

不妨设三边分别为，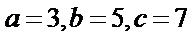

由余弦定理可得，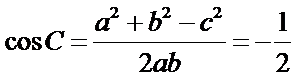

∴，

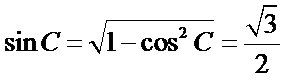
∴由正弦定理可得．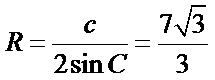

考查方向

解三角形中的正弦定理和余弦定理．

解题思路

已知三边长，先由三角形的余弦定理求得其中一角的余弦值，再根据同角三角比的平方关系求得这个角的正弦值，最后利用三角形的正弦定理，求得该三角形外接圆的半径．

易错点

恰当合理运用正弦定理和余弦定理．

知识点

三角函数中的恒等变换应用

1

题型：简答题

|

简答题 · 13 分

已知函数的图像是由函数的图像经如下变换得到：先将图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移个单位长度.

22.求函数的解析式，并求其图像的对称轴方程；

23.已知关于的方程在内有两个不同的解．

（1）求实数m的取值范围；

（2）证明：

第(1)小题正确答案及相关解析

正确答案

（Ⅰ），

解析

（1）将的图像上所有点的纵坐标伸长到原来的2倍（横坐标不变）得到的图像，再将的图像向右平移个单位长度后得到的图像，故，从而函数图像的对称轴方程为

考查方向

1、三角函数图像变换和性质；2、辅助角公式和诱导公式．

解题思路

有函数的图象变化规律可得到函数的本来面貌，从而求得对称轴方程。

易错点

三角函数变换过程中参数的变换掌握不好，计算能力弱

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）（1）；（2）详见解析．

解析

（2）1）

（其中）

依题意，在区间内有两个不同的解当且仅当，故m的取值范围是.

2）因为是方程在区间内有两个不同的解，

所以，.

当时，

当时,

所以

考查方向

1、三角函数图像变换和性质；2、辅助角公式和诱导公式．

解题思路

结合函数图象，化简三角函数，然后建立不等关系，求出M的取值范围

易错点

计算能力弱，三角函数的图象变换和性质掌握不好，不会利用辅助角公式和诱导公式。

1

题型：简答题

|

简答题 · 14 分

15.在中，AC=6，

（1）求AB的长；

（2）求的值.

正确答案

(1)，为三角形的内角

，即：；

⑵

又为三角形的内角

．

知识点

三角函数中的恒等变换应用

1

题型：简答题

|

简答题 · 4 分

13. 设, ，若对任意实数都有，则满足条件的有序实数组

的组数为______________

正确答案

解析

(i)若

若，则；若，则

(ii)若，若，则；若，则

共组

知识点

三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 6 分

10.已知，则A= ，b= .

正确答案

；1

解析

．，所以

考查方向

三角函数式的两角和与差变换

解题思路

对进行降次，再用辅助角公式。

易错点

没有对进行降次

知识点

三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 4 分

7．方程在区间上的解为__________．

正确答案

或

解析

，即．

∴

∴又∵

∴或

考查方向

三角方程的求解．

解题思路

利用三角公式先将三角方程化为最简形式，然后求最简单的三角方程．

易错点

合理恰当的选择三角公式化简三角方程．

知识点

三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 4 分

14．在锐角三角形中，，为边上的点，与的面积分别为和．过作于，于，则．

正确答案

解析

由题意得：，又,因为DEAF四点共圆，因此.

考查方向

本题考查平面向量的数量积运算，考查了数形结合的解题思想方法，考查了三角函数的化简与求值，是中档题．

解题思路

向量数量积的两种运算方法(1)当已知向量的模和夹角时，可利用定义法求解，即a·b＝|a||b|cos<a，b>．(2)当已知向量的坐标时，可利用坐标法求解，即若a＝(x1，y1)，b＝(x2，y2)，则a·b＝x1x2＋y1y2.向量夹角与三角形内角的关系，可利用三角形解决；向量的模与三角形的边的关系，可利用面积解决.

易错点

准确的化简计算

知识点

三角函数中的恒等变换应用

1

题型：简答题

|

简答题 · 13 分

已知函数f(x)=4tanxsin()cos()-.

15.求f(x)的定义域与最小正周期；

16.讨论f(x)在区间[]上的单调性.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ），

解析

本题属于三角恒等变换与函数性质的综合应用问题，属于简单题，选用恰当的公式，是解决三角问题的关键，明确角的范围，对开方时正负取舍是解题正确的保证. 对于三角函数来说，常常是先化为y＝Asin(ωx＋φ)＋k的形式，再利用三角函数的性质求解．本题只要掌握相关的公式及性质，即可解决本题，具体解析如下：

解：的定义域为.

.

所以, 的最小正周期

考查方向

本题考查了诱导公式、两角差余弦公式、二倍角公式、配角公式、三角函数的单调性等知识点。

解题思路

（Ⅰ）先利用诱导公式、两角差余弦公式、二倍角公式、配角公式将函数化为基本三角函数：，再根据正弦函数性质求定义域、周期

易错点

化简函数解析式时容易出错。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）在区间上单调递增, 在区间上单调递减.

解析

本题属于三角恒等变换与函数性质的综合应用问题，属于简单题，选用恰当的公式，是解决三角问题的关键，明确角的范围，对开方时正负取舍是解题正确的保证. 对于三角函数来说，常常是先化为y＝Asin(ωx＋φ)＋k的形式，再利用三角函数的性质求解．本题只要掌握相关的公式及性质，即可解决本题，具体解析如下：

令函数的单调递增区间是

由,得

设，易知.

所以, 当时, 在区间上单调递增, 在区间上单调递减.

考查方向

本题考查了诱导公式、两角差余弦公式、二倍角公式、配角公式、三角函数的单调性等知识点。

解题思路

根据（1）的结论，研究三角函数在区间[]上单调性。

易错点

化简函数解析式时容易出错。

1

题型：简答题

|

简答题 · 12 分

16.在中，,点D在边上，，求的长.

正确答案

解析

设的内角所对边的长分别是，由余弦定理得

，

所以.

又由正弦定理得.

由题设知，所以.

在中，由正弦定理得.

考查方向

1.正弦定理、余弦定理的应用.

解题思路

设出的内角所对边的长分别是，由余弦定理求出的长度，再由正弦定理求出角的大小，在中.利用正弦定理即可求出的长度.

易错点

正弦定理、余弦定理运用错误，计算错误

知识点

三角函数中的恒等变换应用

1

题型：填空题

|

填空题 · 5 分

9．已知，则=___________

正确答案

解析

-(cos2x-sin2x)=-2cos(2x+π)=2cos［π-(2x+π)］=2cos(-2x)=2cos(2x-),=

考查方向

本题主要考查了辅助角公式。

解题思路

本题考查运用辅助角公式求辅助角，解题步骤如下：

先用辅助角公式得-2cos(2x+π)，再用诱导公式得 2cos(-2x)=2cos(2x-),=

易错点

本题必须注意，忽视则会出现错误。

知识点

三角函数中的恒等变换应用

1

题型：单选题

|

单选题 · 5 分

9．若函数f（x）＝4sinωx·＋cos2ωx（ω＞0）在[－，]上是增函数，则ω的取值范围是（）

A（0，1]

B（0，]

C[1，＋∞）

D[，＋∞）

正确答案

B

解析

由已知得：

是函数含原点的递增区间且函数在上递增，所以有即

因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查了三角函数的诱导公式及单调性，在近几年的各省高考题出现的频率较高，常利用三角函数图像与性质求参数的取值范围来命题。

解题思路

先化简得,由f(x) 区间内单调递增可解得，因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

三角函数在某个给定区间递增或递减，不能正确转化满足条件的不等式。

知识点

正弦函数的单调性三角函数中的恒等变换应用

1

题型：简答题

|

简答题 · 12 分

16.已知向量，设

（I）求函数的解析式及单调增区间；

（II）在中，分别为内角A,B,C的对边，且，求的面积.

正确答案

（1）= []；

（2）

解析

试题分析：本题属于三角函数中的基本问题，题目的难度是逐渐由易到难，直接按照步骤来求

（Ⅰ）

=

由可得

所以函数的单调递增区间为[],

（Ⅱ）

由可得

考查方向

本题考查了利用三角函数的函数单调区间和解三角形求面积

解题思路

本题考查三角函数与解三角形，解题步骤如下：

1、利用向量的数量积求出并求出单调区间；

2、利用余弦定理求出，借助正弦定理求出面积

易错点

第一问中的辅助角容易计算错误

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理平面向量数量积的运算

1

题型：单选题

|

单选题 · 4 分

4．《睡虎地秦墓竹简》记载：“为作务（手工业）及官府市，受钱必辄入其钱缿中，令市者见其入，不从者赀（罚）一甲（铠甲）。”右图所示为“钱缿”。从该题图文不能得出的信息有：（）

①这个“钱缿”可能是陶器

②竹简上的文字字体是楷书

③当时已经出现了民间集市

④政府对市的监管相当严格

A①②

B①④

C②③

D③④

正确答案

C

解析

此题为逆向选择题。根据材料信息“钱缿”图示可知是陶器，“为作务（手工业）及官府市，受钱必辄入其钱缿中，令市者见其入，不从者赀（罚）一甲（铠甲）”可知政府对市的监控管理十分严格。利用排除法，即可得出正确答案。利用所学知识和材料信息，秦代官方字体是篆书，“为作务（手工业）及官府市”反映出官营工商业，所以只有②③符合题干要求，故正确答案选择C项。

考查方向

古代工商官营制度

解题思路

此题为逆向选择题。根据材料信息“钱缿”图示可知是陶器，“为作务（手工业）及官府市，受钱必辄入其钱缿中，令市者见其入，不从者赀（罚）一甲（铠甲）”可知政府对市的监控管理十分严格。利用排除法，即可得出正确答案。利用所学知识和材料信息，秦代官方字体是篆书，“为作务（手工业）及官府市”反映出官营工商业，所以只有②③符合题干要求，故正确答案选择C项。

易错点

本题易错点在于对基础知识的掌握不全面而误选。

知识点

三角函数中的恒等变换应用

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路