- 三角函数与三角恒等变换
- 共3475题
设△






已知
16.求
17.若

正确答案
解析
解:由


∴

考查方向
解题思路
可直接将题中的等式关系,用正弦定理将边的关系转成角的关系,再结合两角和公式,求出角A
易错点
问题容易在利用均值不等式放缩时出错
正确答案
解析
解:由

∴
∴
∴

又由题意知:
故:
考查方向
解题思路
可根据余弦定理, 得到b,c关系的等式, 再利用均值不等式进行合理缩放,可求出b+c取值范围
易错点
问题容易在利用均值不等式放缩时出错
在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及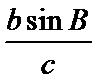
正确答案
∠A=60°;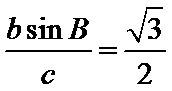
考查方向
易错点
1、对a、b、c成等比结合a2-c2=ac-bc的化简方向的选择
知识点
3. 已知


正确答案
解析




所以

考查方向
解题思路
1.先根据题中条件求出角
易错点
1.利用诱导公式在化简时出错;2.对于特殊角的三角函数值记忆出错。
知识点
4.在



正确答案
解析
由题意及正弦定理得




考查方向
解题思路
1.先根据正弦定理将角化为边;2.利用余弦定理求出角C即可。
易错点
1.不知道该将

知识点
已知函数
15.确定
16.求函数

正确答案
(1)2;
解析
(Ⅰ)
因为最小正周期
所以
考查方向
解题思路
先将函数化简为一个角的一个三角函数的形式,然后利用周期即可求得答案;
易错点

正确答案
(2)最大值为1,最小值为
解析
(Ⅱ)






故函数


考查方向
解题思路
先判断函数的增减性,然后即可求得最大值和最小值。
易错点
直接将端点值带入求解得到值域,没有考虑到函数的单调出错。
11.已知函数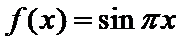
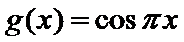
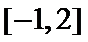
正确答案
解析
由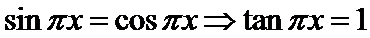
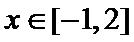
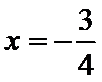
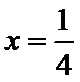
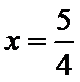
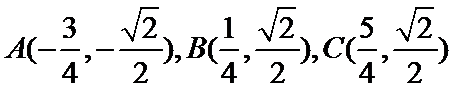
故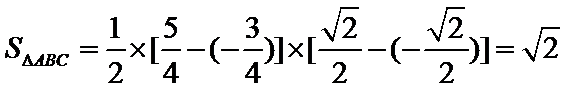
考查方向
解题思路
1.先根据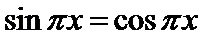
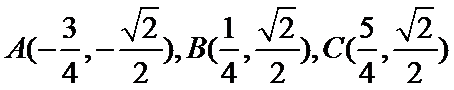
易错点
1.不会结合图像求出A,B,C的坐标;2.不会做函数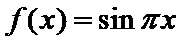
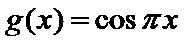
知识点
4.已知



正确答案
解析
函数图像的一个最高点与其相邻的一个最低点的距离为5,可求得水平距离为3,所以周期为6,则

考查方向
解题思路
先求周期为6, 再由公式求出
易错点
容易将题中的距离理解为水平距离,而错选C
知识点
9.已知角



正确答案
-2,
解析
由三角函数定义,可知角











考查方向
解题思路
根据三角函数的定义,解出tan
易错点
定义理解不到位,公式应用错误
知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
已知函数
20.求函数

21.设






正确答案
当

解析
要使





考查方向
解题思路
解题步骤如下:
易错点
本题易在利用倍角公式变形时发生错误 。
正确答案
解析
考查方向
解题思路
易错点
本题易在利用倍角公式变形时发生错误 。
2.在


正确答案
解析
因为


因为

考查方向
解题思路
先由

易错点
本题易在由

知识点
4.设

正确答案
解析
sin







考查方向
解题思路
将左边化为


易错点
诱导公式,辅助角公式,求解不等式
知识点
5.在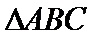
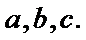
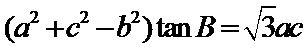
正确答案
解析
由余弦定理,知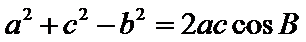
所以,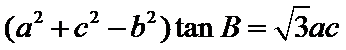
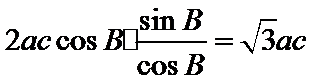
所以,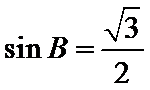
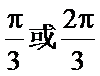
故选C。
考查方向
解题思路
由条件得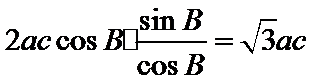
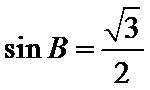
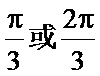
易错点
本题在把题意转化成余弦定理模型上易出错。
本题容易忽视正弦在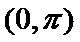
知识点
已知向量m



20.求函数

21.设






正确答案
当

解析








考查方向
解题思路
解题步骤如下:利用向量的坐标运算、倍角公式、辅助角公式把函数



易错点
本题易在利用倍角公式变形时发生错误 。
正确答案
解析
由题意,得





考查方向
解题思路
解题步骤如下:由



易错点
本题易在利用倍角公式变形时发生错误 。
10.如图所示,函数



正确答案
解析
设两个交点为A、B,由抛物线图象可知,令y=0,解得交点A(-









考查方向
解题思路
先根据两个图像的特殊性,求出两个交点的坐标,AB两点的水平距离恰为1/4周期,应用周期公式求出

易错点
不能正确的提炼图像中渗透的信息,没有掌握抛物线,二次函数图特殊性.
知识点
扫码查看完整答案与解析