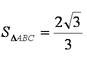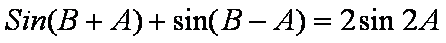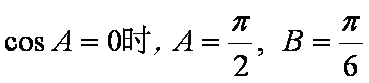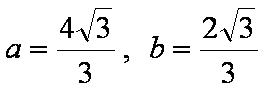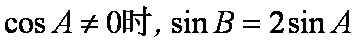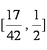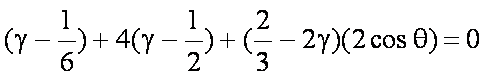- 三角函数与三角恒等变换
- 共3475题
已知函数

(1) 求f(x)的解析式;
(2)在△ABC中,AC=2,BC=3,A为锐角,且
正确答案
见解析。
解析
(1)
(2)


知识点
在△ABC中,内角A、B、C对边的边长分别是a、b、c,已知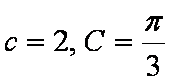
(1)若△ABC的面积等于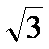
(2)若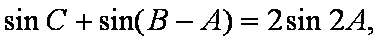
正确答案
(1)a=2,b=2(2)
解析
(1)由余弦定理及已知条件得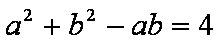
又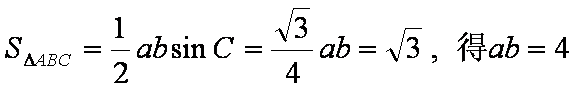
① ②联立解得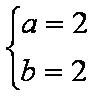
(2)由题设得
即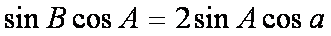
当
根据正弦定理,得
此时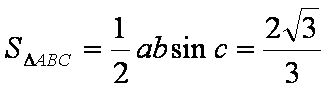
当
由正弦定理,得 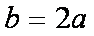
联立①与③解得 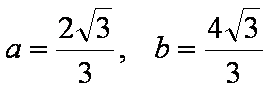
此时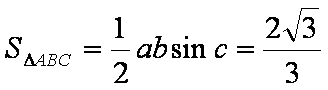

知识点
命题“若α=
正确答案
解析
命题:“若α=
故选C
知识点
在







正确答案
见解析。
解析
。在


所以
又

因为



所以,

由①、②可知 
所以
知识点
在△OAB的边OA、OB上分别有一点P、Q,已知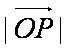
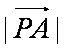
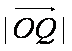
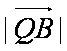
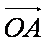
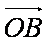
(1)用a与 b表示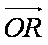
(2)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角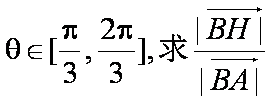
正确答案
(1)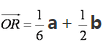
解析
解析:(1)由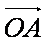
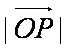
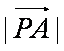
可得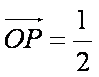
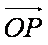
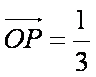
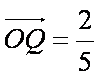
设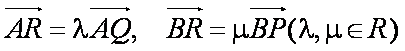
则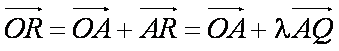
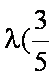
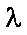
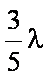
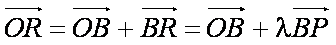
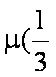
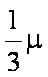
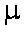
∵向量a与b不共线, ∴
∴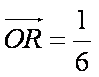

(2)设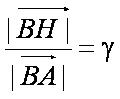
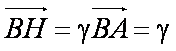
∴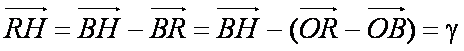


=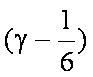
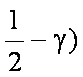
∵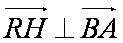
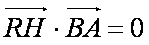
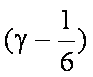
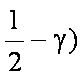
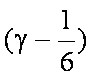
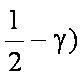
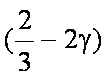
又∵|a|=1, |b|=2, a·b=|a||b|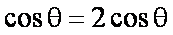
∴
∴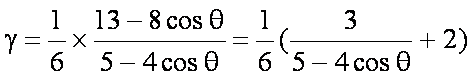
∵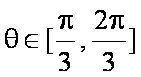
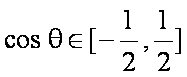

∴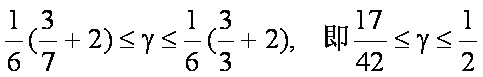
故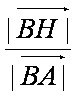
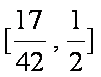
知识点
在等腰梯形












正确答案
解析
如图,过













故
知识点
在△ABC中,角A、B、C的所对应边分别为a,b,c,且
(1)求c的值;
(2)求
正确答案
见解析
解析
解:(1)根据正弦定理,
(2)根据余弦定理,得
于是
所以
知识点
在△ABC中,角A,B,C的对边分别为a,b,c。
(1)若cos(A+
(2)若cosA=
正确答案
见解析
解析
(1)在△ABC中,若cos(A+


化简可得



(2)若cosA=

由于sinA=



知识点
设数列




(1)若


(2)求
正确答案
见解析
解析
(1)在



由
相减可得


可见,

(2)由


即当

① 若



故
② 若
③ 若



于是当








知识点
设an=

正确答案
解析
由于f(n)=sin
由正弦函数性质可知,a1,a2,…,a24>0,a25=0,a26,a27,…,a49<0,a50=0
且sin


a26…a50都为负数,但是|a25|<a1,|a26|<a2,…,|a49|<a24
∴ S1,S2,…,S25中都为正,而s26,s27,…,s50都为正
同理S1,S2,…,s75都为正,S1,S2,…,s75,…,s100都为正,
故选D
知识点
甲、乙等五名大冬会志愿者被随机地分到黑大、体院、理工、亚布力四个不同的比赛场馆服务,每个场馆至少有一名志愿者。
(1)求甲、乙两人同时到黑大场馆服务的概率;
(2)设随机变量

正确答案
见解析
解析
(1)记甲、乙两人同时到黑大场馆服务为事件A,那么
即甲、乙两人同时到黑大场馆服务的概率是
(2)随机变量
事件“
则
所以


知识点
已知函数

(1)当

(2)若

(3)对于


证明:
正确答案
见解析
解析
(1)由

令





当



故

(2)



当

对于

当



当



于是

只需

∵



则



(3)解法1:
由已知得:

先证


设



∴

同理可证

解法2:
令

下面证明
令



构造函数






同理可证
即

得



同理,在区间


由
知识点
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示,该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个丌学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润。
(1)将Y表示为X的函数;
(2)根据直方图估计利润Y不少于4800元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区的频率作为需求量取该区间中点值的概率(例如:若需求量X
正确答案
见解析
解析
(1)
(2)
(3)根据题意得 获得利润Y的分布列是
所以数学期望为
知识点
如图,四棱锥P-ABCD 的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(1)证明:AC⊥DE;
(2)若PC=BC,求二面角E-AC-P的余弦值。
正确答案
见解析
解析
解析:解:(1)∵PD⊥平面ABCD,∴PD⊥AC,
∵底面ABCD是正方形,∴BD⊥AC,∴AC⊥平面PBD,
∵DE⊂平面PBD,∴AC⊥DE.(5分)
(2)以D为原点,DP,DA,DC所在的直线为x,y,z轴建立空间直角坐标系。
设BC=3,则CP=3,DP=3,因为2BE=EP,
易知D(0,0,0),A(0,3,0),C(0,0,3),P(3,0,0),E(1,2,2)。
所以→(CA)=(0,3,-3),→(CP)=(3,0,-3),→(CE)=(1,2,-1),
设平面ACP的法向量为u=(x,y,z),则u·→(CA)=0,u·→(CP)=0,
即3x-3z=0,(3y-3z=0,)令x=1,得u=(1,1,1),同理可取平面ACE的法向量v=(-1,1,1),
所以cos〈u,v〉=|u||v|(u·v)=3(1),由图知二面角E-AC-P为锐二面角,所以二面角E—AC—P的余弦值为3(1).(12分)
知识点
如图,圆o1和圆o2相交于A,B两点,AB是圆o2的直径,过点A作圆O1的切线交圆O2于点E,并与BO1的延长线变于点P,分别与O1,O2交于C,D两点。
证明:
(1)PA·PD=PE·PC;
(2)AD=AE。
正确答案
见解析
解析
(1)因为


又


由①②得
(2)连接











知识点
扫码查看完整答案与解析