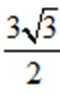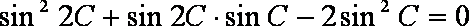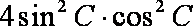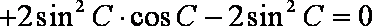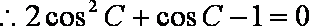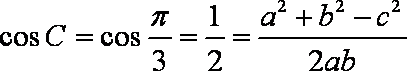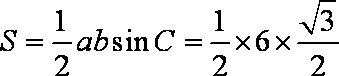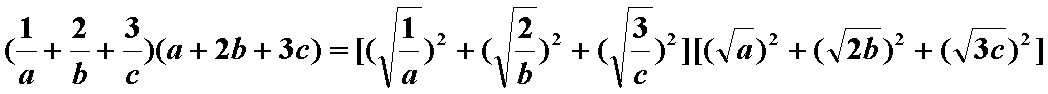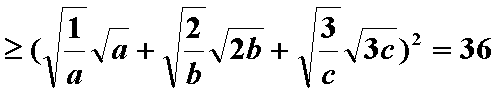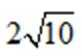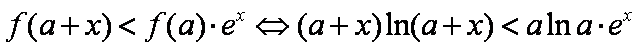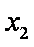- 三角函数与三角恒等变换
- 共3475题
在
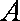
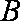
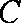
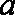
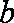
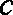
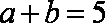
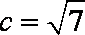
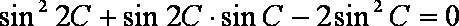
(1)求角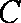
(2) 求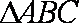
正确答案
(1)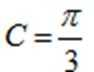
解析
(1)∵
∴
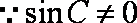
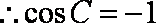
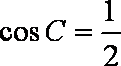
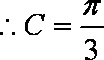
(2)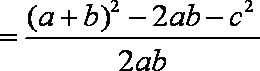
又∵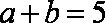
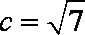
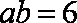
∴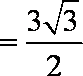
知识点
某企业拟在










(1)将


(2)该企业
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
正确答案
见解析
解析
解析:(1)由题意:

∴
当年生产

当销售


由题意,生产
∴年利润=年销售收入-年生产成本-促销费
即
(2)∵
当且仅当


∴当促销费定在
知识点
已知曲线C1的极坐标方程为ρcos(θ-
2

(1)求曲线C2的直角坐标方程;
(2)求曲线C2上的动点M到曲线C1的距离的最大值。
正确答案
见解析
解析
解析:
(1)
即

故

(2)

由(1)知曲线



所以动点

知识点
设集合




正确答案
解析
识别条件:
转念:这个集合中放的是点坐标! 满足
这个是啥东西? 是一个菱形,也是正方形,中心在坐标原点。 集合A中就是这个正方形内部的点。分象限逐一讨论 这个应该是平时练习过的一个知识点 还有比这个复杂的
继续识别条件:
继续识别条件:从集合





知识点
已知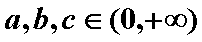
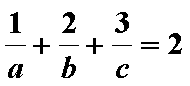
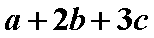
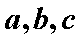
正确答案
见解析
解析
又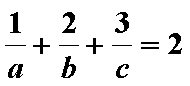
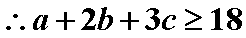
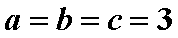
当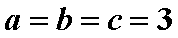
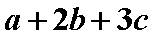
知识点
已知不等式2|x-3|+|x-4|<2a。
(1)若a=1,求不等式的解集;
(2)若已知不等式的解集不是空集,求a的取值范围。
正确答案
见解析
解析
解析:
(1)当

若



若


若


综上,不等式的解集为
(2)设





知识点
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,
(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.
正确答案
见解析
解析
(1)因为四边形ABCD是菱形,
所以AC
因为PA
所有PA
又因为PA
所以BD
而BD
所以面PBD
(2)如图,设AC
在△APC中,AO=OC,CQ=QP,OQ为△APC的中位线,所以OQ//PA.
因为PA
所以OQ
以OA、OB、OQ所在直线分别为

则

因为BO
所以平面PAC的一个法向量为
设平面PBC的一个法向量为
而
由
令
所以



知识点
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC//平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
(1)求证:四点B、C、F、G共面;
(2)求平面ADGC与平面BCGF所组成的二面角余弦值;
(3) 求多面体ABC-DEFG的体积.
正确答案
见解析
解析
由 AD⊥面DEFG和直角梯形EFGD可知,AD、DE、DG两两垂直,建立如图的坐标系,则A(0,0,2),B(2,0,2),C(0,1,2),E(2,0,0),G(0,2,0),F(2,1,0)
(1)
∴
故四点B、C、F、G共面. ……………………4分
(2)
设平面BC

则
令

而平面ADGC的法向量
∴

故面ADGC与面BCGF所组成的二面角余弦值为
(3)设DG的中点为M,连接AM、FM,则
=


解法二 (1)设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,所以MF//DE,且MF=DE
又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,且BF=AM

∴AC//MG,且AC=MG,即四边形ACGM是平行四边形
∴GC//AM,且GC=AM
故GC//BF,且GC=BF,
即四点B、C、F、G共面………………4分
(2)∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴M
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴



∴
在直角三角形MNF中,MF=2,MN
∴




故面ADGC与面BCGF所组成的二面角余弦值为
(3)




知识点
以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,并在两种坐标系中取相同的单位长度。已知直线l的极坐标方程为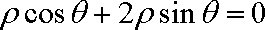
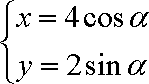
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)若直线l与曲线C交于A、B两点,求线段AB的长。
正确答案
(1)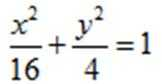
解析
(1)直线l的直角坐标方程为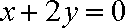
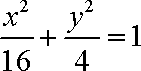
(2)可求得交点坐标为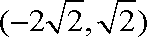
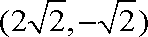
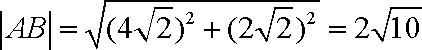
知识点
若变量x,y满足约束条件

正确答案
答案:6
解析
略
知识点
若



正确答案
解析
略
知识点
已知函数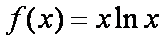
(1)讨论函数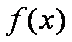
(2)对于任意正实数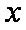
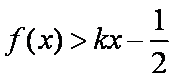
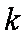
(3)是否存在最小的正常数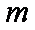
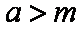
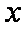
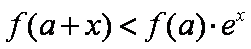
正确答案
见解析。
解析
(1)令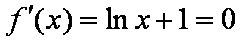
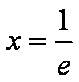
当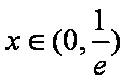
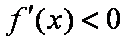
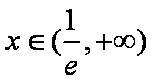
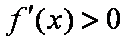
所以函数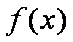
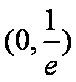
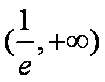
(2)由于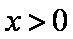
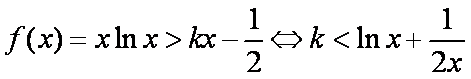
构造函数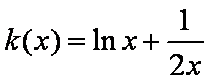
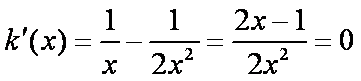
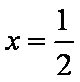
当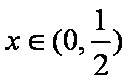
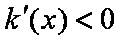
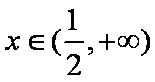
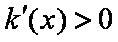
所以函数在点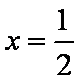
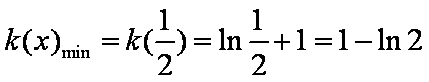
因此所求的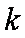
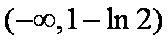
(3)结论:这样的最小正常数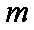
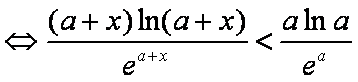
构造函数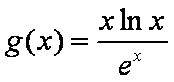
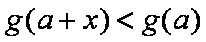
对于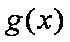
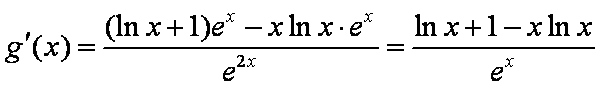
令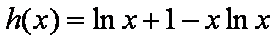

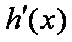
又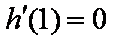
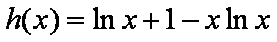
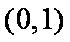
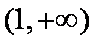
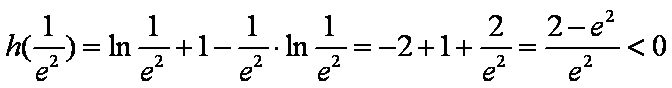
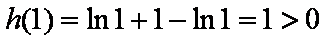
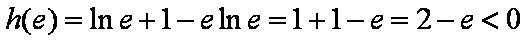
所以函数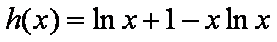
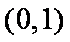
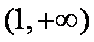
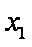
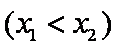
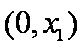
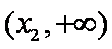
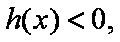
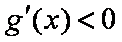
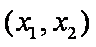
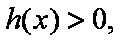
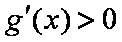
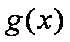
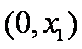
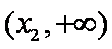
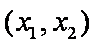
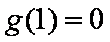
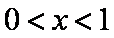
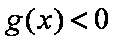

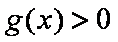
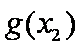
题目要找的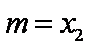
当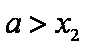
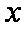
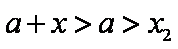
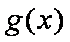
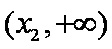
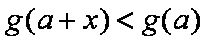

当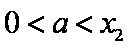
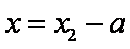

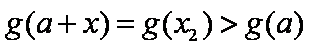
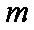
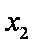
综合可知,题目所要寻求的最小正常数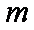
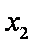
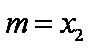
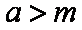
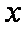
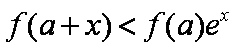
( 注意:对于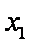
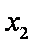
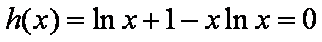
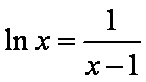
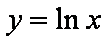
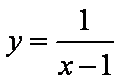
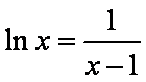
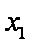
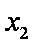
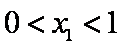
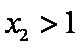
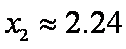
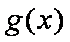
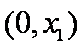
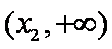
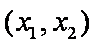
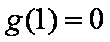
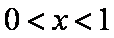
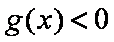
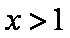
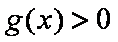
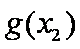
知识点
若函数





(1)已知函数


(2)记向量






(3)对于函数

正确答案
见解析
解析
(1)

依题意得

∴

(2)依题意,
将
得到函数
再将所得的图象上所有点向左平移

即
∵

∵


∴
………………10分
(3)若函数
则存在


令

因此


显然上式对任意的
所以函数
(注:本题若化成
知识点
已知平面的一条斜线






正确答案
解析
由最小角定理
知识点
已知函数





(1)求函数
(2)若

正确答案
见解析
解析
解析:(1)
由

由
(2)由

又




知识点
扫码查看完整答案与解析