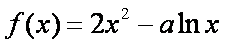- 三角函数与三角恒等变换
- 共3475题
在直角坐标平面内,将每个点绕原点按逆时针方向旋转





(1)求矩阵

(2)求曲线


正确答案
见解析
解析



(2)




故所求的曲线方程为:
知识点
小明打算从







(1)求小明选择
(2)设

正确答案
见解析
解析
(1)设小明选择



即

(2)依题意得

∴

知识点
已知函数

正确答案
m>1
解析
函数






知识点
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆O于点E、F,点M在EF上,且
(1)求证:PA·PB=PM·PQ
(2)求证:
正确答案
见解析
解析
解析:(1)∵∠BAD=∠BMF,
所以A,Q,M,B四点共圆,……………3分
所以
(2)∵
∴
又 

∴

∵
∴

所以
知识点
已知函数
(1)若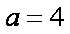
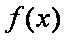
(2)设函数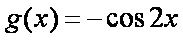
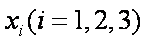
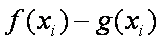
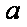
正确答案
见解析
解析
(1)由已知得
则当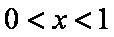
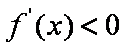
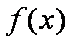
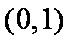
当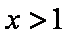
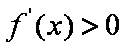
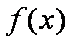
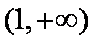
故函数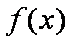
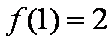
(2)若存在,设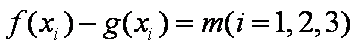
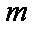
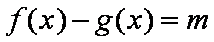
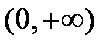
设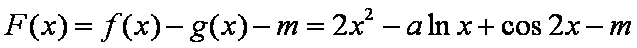
则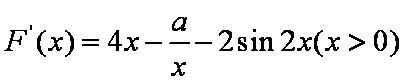
方法一: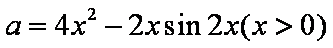
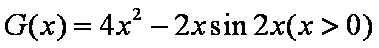
则
设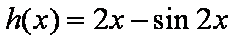
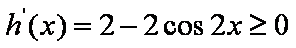
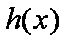
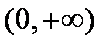
则当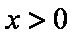
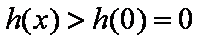
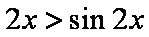
又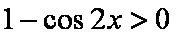
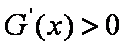
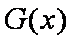
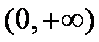
则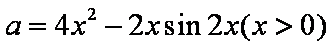
方法二:关于方程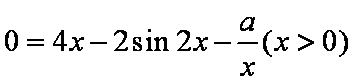
当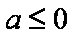
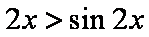
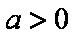
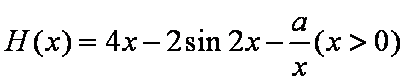
知识点
17.随机变量X的分布列如下表如示,若数列



(1)求随机变量X的分布列;
(2)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
正确答案
见解析。
解析
(1)依题意得,数列


(2)随机抽取一次取得标签的标号不大于3的概率为


所以恰好2次取得标签的标号小于3的概率为

知识点
已知函数
(1)若
(2) 若曲线




正确答案
见解析。
解析
(1)
又f(2)=ln3-1,f(4)=1+ln5,

(2)函数

所以曲线

因为切线与曲线有唯一的公共点,
所以方程

令
则
① 当a=1时,
② 当a
在区间

在区间
而
因此

即当
知识点
设函数


正确答案
解析

因为



从而有

知识点
如图,已知矩形






(1)求证:

(2)求二面角
正确答案
见解析
解析
解析:(1)建立如图所示的空间直角坐标系,
则



取



所以




……………………………………………6分
(2)由(1)知平面




所以向量





知识点
6.有5名优秀毕业生到母校的3个班去作学习经验交流,则每个班至少去一名的不同分派方法种数为( )
正确答案
解析
人数分配上有两种方式即1,2,2与1,1,3.
若是1,1,3,则有



所以共有150种不同的方法.故选:A.
知识点
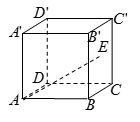
20.如图所示,已知单位正方体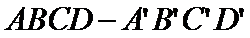
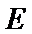
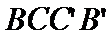
(1)求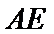
(2)求异面直线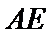
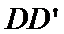
(3)求二面角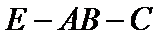
正确答案
(1)过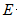
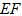
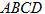

∴ 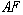
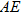
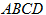
∴∠ 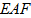
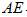
∴在 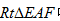
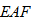

因此,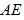
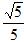
(2)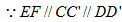
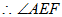
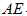
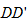
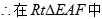
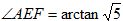
因此,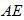
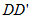
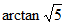
(3)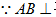
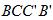
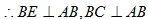
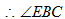
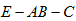
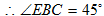
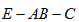
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 执行下边的程序框图,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.△ABC的内角A,B,C把对的边a,b,c且ccosB与bcosC的等差中项为2acosA。
(1)求cosA的值;
(2)若△ABC的面积是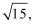
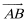
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知









正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析