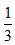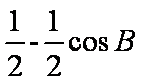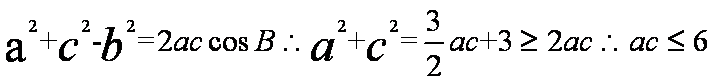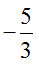- 三角函数与三角恒等变换
- 共3475题
已知函数

(1)求

(2)求函数

正确答案
见解析
解析

(1)


(2)令


又因为




知识点
已知a是第二象限的角,
正确答案
解析
知识点
如果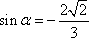
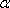
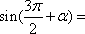
正确答案
解析
略
知识点
在

正确答案
解析
略
知识点
函数
正确答案
解析
略
知识点
在




正确答案
解析
略
知识点
已知△ABC中,角A、B、C的对边分别
(1)求
(2)求
正确答案
见解析。
解析
(1)
由余弦定理得
(2)由正弦定理知:
知识点
如图, 平面









(1) 设



(2) 证明:在






正确答案
见解析
解析
解析:证明:
(1)如图, 连结OP, 以O为坐标原点, 分别以OB、OC、 OP所在直线为





由题意得, 

因此平面BOE的法向量为




因此有

(2)设点M的坐标为





在平面直角坐标系






由点M的坐标得点





知识点
“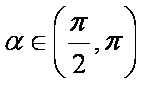
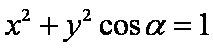
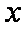
正确答案
解析
当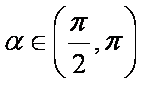
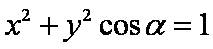
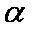
知识点
已知函数





(1)求a的值;
(2)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,



正确答案
见解析
解析
解析:(1)因为
所以
因为h(x)在区间
所以

若0<a<1,则lna<0,于是
又
由

所以lna=1,即a=e。
(2)由(1),


以下证明
(※)等价于
令



当


从而
对于

知识点
在三角形ABC中,角A,B,C的对边分别为a,b,c,且cosB=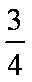
(1)求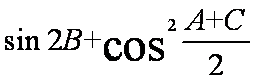
(2)若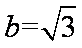
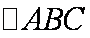
正确答案
(1)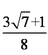
解析
解析:(1)
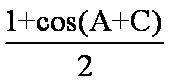
由cosB=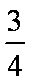
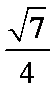

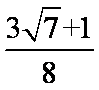
(2)由余弦定理得
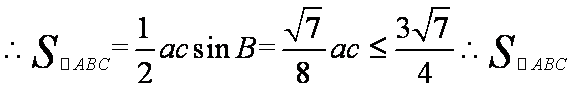
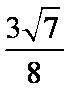
知识点
设函数
(1)求函数f(x)在点
(2)设

(3)设函数



正确答案
(1)


(3)存在实数m=1和M=2,使得对每一个

解析
(1)解:



(2)


令


①当0<



令

所以,F(x)在(0,




②当


所以,F(x)在(0,+
③当

所以,F(x)在(0,




(3)

当x在区间

又
据经可得,若


并且对每一个


综上,存在实数m=1和M=2,使得对每一个

知识点
已知函数
(1)求
(2)在


正确答案
(1)1(2)
解析
解析:(1)


(2)



知识点
一个口袋中装有大小相同的



(1)试用

(2)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为

(3)在(2)的条件下,将







正确答案
见解析
解析
解析:(1)一次摸奖从

它们是等可能的,其中两个球的颜色不同的方法有
一次摸奖中奖的概率为
(2)设每次摸奖中奖的概率为





因而



∴当



(3)由(2)知:记上





知识点
已知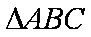
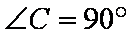
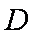
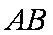
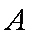
(1)设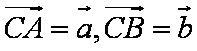
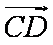
(2)若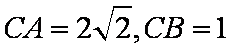
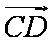
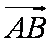
正确答案
(1)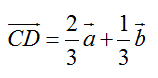
解析
解析:(1) ∵ 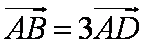
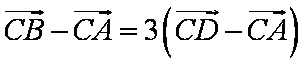
∴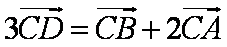
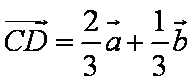
(2)过C作
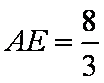
又因为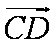
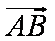
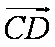
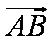
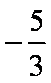
知识点
扫码查看完整答案与解析