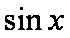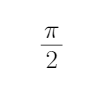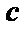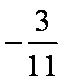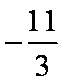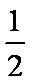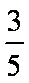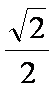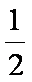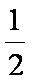- 三角函数与三角恒等变换
- 共3475题
在



(1)求角
(2)若

正确答案
见解析
解析
(1)由已知得
∴


(2)法一:由余弦定理得
∴

解得
又

∴

法二:由正弦定理得
又



∵

∴

知识点
已知数列






(1)求

(2)若对任意的


正确答案
(1)
解析
(1)在
得

(2)1)当







2)当n为奇数时,要使不等式






综合(1)(2)可得


知识点
一个三棱柱的正(主)视图和侧(左)视图分别是矩形和正三角形,如图所示,则这个三棱柱的体积为_________;
正确答案
解析
由正视图和侧视图可知,这是一个水平放置的一个正三棱柱,底面正三角形的高为

知识点
已知函数
(1)当
(2)求函数f (x)的定义域与值域。
正确答案
(1)
(2)当


当

解析
(1)由
又∵
令



(2)由
∵ 函数的定义域不能为空集,故

令
①当





∴ 


②当


∴ 


综上:当


当


知识点
在数列

(1)求数列
(2)求证:数列
(3)设数列



正确答案
见解析
解析
(1)∵
∴数列{


∴
(2)∵
∴
∴
∴数列


(3)由(1)知,


∴
∴
于是
…………………………………………………………………………………………… 9分
两式①-②相减得
=
∴ 
知识点
以椭圆











正确答案
解析
略
知识点
若方程

正确答案
解析
方程
等价于求
∵
则
知识点
复数
正确答案
解析
由题
知识点
在极坐标系中,曲线
正确答案
解析
略
知识点
社区主任要为小红等4名志愿者和他们帮助的2位老人拍照,
正确答案
答案:24
解析
略
知识点
函数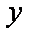
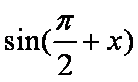
正确答案
解析
略
知识点
已知
cosA=

(1)求tanC的值;
(2)若a=

正确答案
见解析
解析
(1)∵cosA=

又
=

整理得:tanC=
(2)由(1)知sinC=
由正弦定理知:

又∵sinB=

∴


知识点
已知

正确答案
解析
略
知识点
已知向量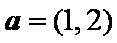
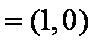
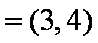
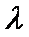
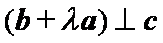
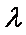
正确答案
解析
函数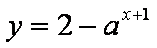
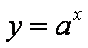

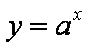
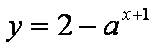
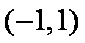
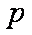
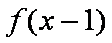
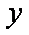
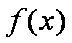
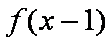
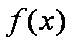
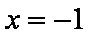
知识点
在ABC中,若tanAtanB= tanA+ tanB+ 1,则cosC的值是
正确答案
解析
由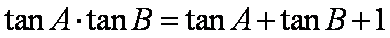
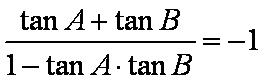
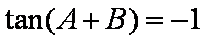
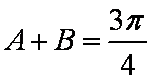
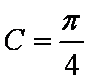
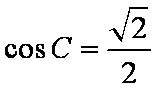
知识点
扫码查看完整答案与解析