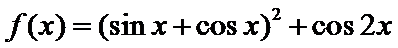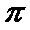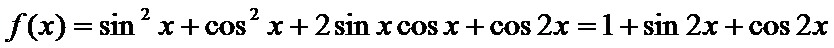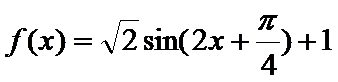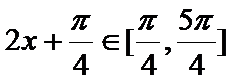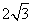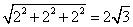- 三角函数与三角恒等变换
- 共3475题
已知函数
16.求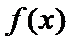
17.求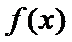
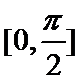
正确答案
(Ⅰ)
解析
(Ⅰ)因为
所以函数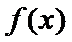
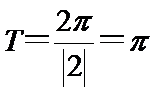
考查方向
解题思路
先化简,然后再求出三角函数的最小正周期
易错点
三角函数化简时错误
正确答案
(Ⅱ)最大值为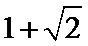
解析
(Ⅱ)由(Ⅰ)得计算结果,
当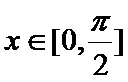
由正弦函数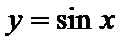
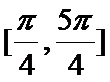
当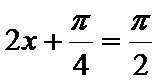
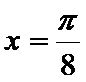
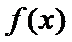
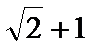
当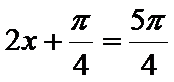
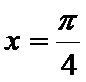
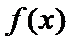

综上,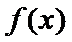
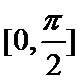

考查方向
解题思路
根据第一问结果,结合函数图象判断求解
易错点
根据第一问求出的一般形式判断函数最值
11.设









正确答案

解析
因为









考查方向
解题思路
先根据题目直接算出角B的大小,角A的大小,然后再用正弦定理直接解得b的值。
易错点
常见的正弦函数值要记清楚。
知识点
11.罗斯福“新政”时期,曾颁布某项法案,到1935年初“它使大约200万失业者有了工作;它帮助制止了通货膨胀的重新加剧;它有助于促进企业道德和提倡文明竞争;„„它在很大程度上取消了童工和血汗工厂”。下列各项中与该规定属于同一法案的是
正确答案
解析
根据材料信息我们可以知道该法案可以“失业者有了工作”“制 止了通货膨胀的重新加剧”“ 促进企业道德和提倡文明竞争”“ 很大程度上取消了童工和血汗工厂”,可以推断出来该法案即《全国工业复兴法》,根据所学我们知道该法案规定了工业发展规则:按规定的市场分配销售产品、保持同类企业间产品价格的稳定、给予工人集体谈判的权利等等,所以正确答案选择D项。A项、B项、C项都不符合材料信息。
考查方向
解题思路
根据材料信息我们可以知道该法案可以“失业者有了工作”“制 止了通货膨胀的重新加剧”“ 促进企业道德和提倡文明竞争”“ 很大程度上取消了童工和血汗工厂”,可以推断出来该法案即《全国工业复兴法》,根据所学我们知道该法案规定了工业发展规则:按规定的市场分配销售产品、保持同类企业间产品价格的稳定、给予工人集体谈判的权利等等,所以正确答案选择D项。A项、B项、C项都不符合材料信息。
易错点
本题易错点在于对教材知识掌握不准确而误选
知识点
某石油开采企业2004年2月开采原油20万吨,其中用于加热、修井的原油0.2万吨。如油田的资源税税率为10元/吨。该企业当月应缴纳的资源税税额为( )万元。
A.198
B.297
C.200
D.300
正确答案
A
解析
开采原油过程中用于加热、修井的原油免税。(20-0.2)×10=198(万元)。
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为



正确答案
解析
略
知识点
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为________。
正确答案
1
解析
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cos φ-cos(x+φ)sin φ=sin x,故其最大值为1.
知识点

正确答案
解析
原式=
知识点
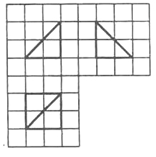
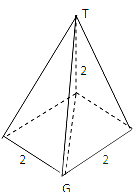
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
正确答案
解析
由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为
知识点
13. 在





正确答案

解析
由






考查方向
解题思路
由

易错点
考查知识点相对较多,基础不扎实,对个别公式掌握不熟练而出错。
知识点
设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6)。
(1)确定a的值;
(2)求函数f(x)的单调区间与极值。
正确答案
(1) 

解析
(1)因f(x)=a(x-5)2+6ln x,
故f′(x)=2a(x-5)+
令x=1,得f(1)=16a,f′(1)=6-8a,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-16a=(6-8a)(x-1),由点(0,6)在切线上可得6-16a=8a-6,故
(2)由(1)知,f(x)=
f′(x)=x-5+

令f′(x)=0,解得x1=2,x2=3.
当0<x<2或x>3时,f′(x)>0,故f(x)在(0,2),(3,+∞)上为增函数;当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数。
由此可知f(x)在x=2处取得极大值f(2)=
知识点
若函数
正确答案
解析
略
知识点
设a>0.若曲线
正确答案
解析


知识点
在△ABC中,


(1)求角A的大小;
(2)设函数


正确答案
见解析。
解析
(1)在

可得
∵

∴
(2)

∵

∴当


又∵


知识点
若a,b均为实数,且方程

正确答案
解析
略
知识点
扫码查看完整答案与解析