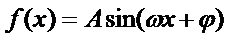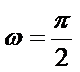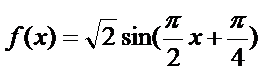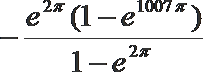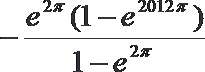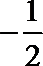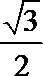- 三角函数与三角恒等变换
- 共3475题
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若正四棱锥的正视图如右图所示,则该正四梭锥体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
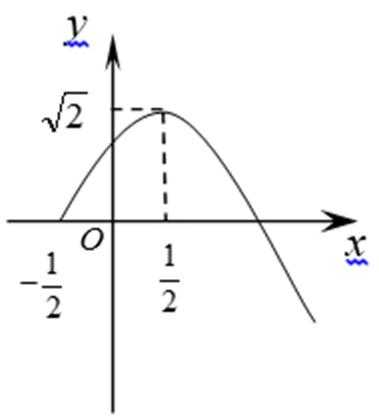
19.若函数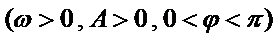
(1)求出函数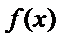
(2)求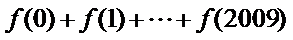
正确答案
(1)由图知:
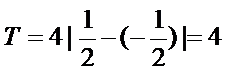
∴ 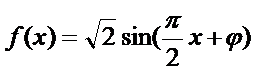
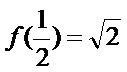
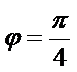
∴
(2)由(1)得 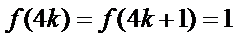
∴ 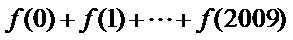
解析
解析已在路上飞奔,马上就到!
知识点
15.△ABC 中 A 为锐角,且
(1)求 
(2)若 


正确答案
(1)(
(2) 

解析
解析已在路上飞奔,马上就到!
知识点
9. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知抛物线










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某旅游景点有一处山峰,游客需从景







(1)求B,D两点的海拔落差
(2)求AD的长.
正确答案
解:(1)
(2)法一:在

在

所以
法二:在

所以
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数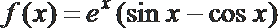
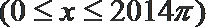
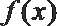
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在等差数列


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数


(1)求a、b的值;
(2)若对于任意的

正确答案
(1)
解得
(2)由(1)可知,
当
即




又
故当


于是有

因此
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


(1)求函数
(2)若


正确答案
(1)




函数



解析
解析已在路上飞奔,马上就到!
知识点
2.已知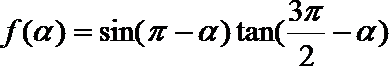
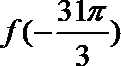
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生必须在22、23题中任选一题做答。
22.
在
(1)求证:
(2)若AC=3,求
23.已知对于任意非零实数


正确答案
22.
解:(1)


又
(2)


23.
解:即


(1)当


(2)当


(3)当



综上

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析