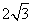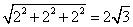- 三角函数与三角恒等变换
- 共3475题
18.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知角






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在


(1) 求证:
(2) 若
正确答案
(1)由 
即
整理得:
所以
又
所以
(2)由(1)及
可得
又
所以
所以三角形ABC的面积
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数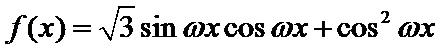
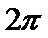
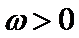
(Ⅰ)求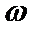
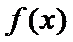
(Ⅱ)在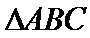
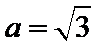
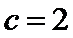
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知sin α·sin β=1,那么cos(α+β)的值是( )
正确答案
解析
由sin α·sin β=1,
得
那么
因此
知识点
19.(1)求证:sinα·sinβ=
(2)在锐角△ABC中,∠ A=60°,BC=2,求△ABC面积的取值范围.
正确答案
(1)略;
(2)
解析
本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
(1)由

两式相减得:
(2)由正弦定理可知,
由
所以
考查方向
本题考查了三角函数的积化和差的证明及解三角形的问题.属于高考中的高频考点。
解题思路
无
易错点
注意锐角三角形的条件,忽视则容易出错。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
4.




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若关于x的方程


正确答案
[-3,9]
解析
解析已在路上飞奔,马上就到!
知识点
19.(1)求证:sinα·sinβ=
(2)在锐角△ABC中,∠ A=60°,BC=2,求△ABC面积的取值范围.
正确答案
(1)略;
(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
(1)由

两式相减得:
(2)由正弦定理可知,
由
所以
考查方向
本题考查了三角函数的积化和差的证明及解三角形的问题.属于高考中的高频考点。
解题思路
本题考查三角函数问题,解题步骤如下:
(1)利用两角和差公式证明。
(2)利用正余弦定理求解。
易错点
注意锐角三角形的条件,忽视则容易出错。
知识点
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为



正确答案
解析
略
知识点
设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6)。
(1)确定a的值;
(2)求函数f(x)的单调区间与极值。
正确答案
(1) 

解析
(1)因f(x)=a(x-5)2+6ln x,
故f′(x)=2a(x-5)+
令x=1,得f(1)=16a,f′(1)=6-8a,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-16a=(6-8a)(x-1),由点(0,6)在切线上可得6-16a=8a-6,故
(2)由(1)知,f(x)=
f′(x)=x-5+

令f′(x)=0,解得x1=2,x2=3.
当0<x<2或x>3时,f′(x)>0,故f(x)在(0,2),(3,+∞)上为增函数;当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数。
由此可知f(x)在x=2处取得极大值f(2)=
知识点
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为________。
正确答案
1
解析
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cos φ-cos(x+φ)sin φ=sin x,故其最大值为1.
知识点

正确答案
解析
原式=
知识点
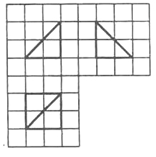
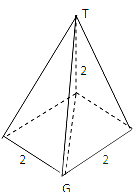
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
正确答案
解析
由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为
知识点
扫码查看完整答案与解析