- 三角函数与三角恒等变换
- 共3475题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数f(x)





正确答案
解析
因为当

当





知识点
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响。 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用
(1)记“函数



(2)求
正确答案
见解析。
解析
(1)设该学生选修甲、乙、丙的概率分别为

依题意得
若函数



表示该学生选修三门功课或三门功课都没选。



(2)依题意知

∴

知识点
已知实数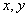
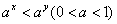
正确答案
解析
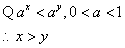
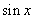
知识点
已知向量m=(sinx,1)
(1)求A;
(2)将函数y=f(x)的图象像左平移


正确答案
见解析。
解析
(1)
则
(2)函数y=f(x)的图象像左平移

再将所得图象各点的横坐标缩短为原来的

当


故函数g(x)在

知识点
函数


(1)求函数
(2)设


正确答案
见解析
解析
(1)∵函数


∵函数图像的相邻两条对称轴之间的距离为


故函数

(2)∵

∵



知识点
设三棱柱的侧棱垂直于底面,所有棱的长都为
正确答案
解析
设该球的半径为

因此该球的表面积为
知识点
设复数


正确答案
解析
略
知识点
已知函数f(x)=alnx﹣bx2图象上一点P(2,f(2))处的切线方程为y=﹣3x+2ln2+2。
(1)求a,b的值;
(2)若方程f(x)+m=0在
(3)令g(x)=f(x)﹣kx,若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),AB的中点为C(x0,0),求证:g(x)在x0处的导数g′(x0)≠0。
正确答案
见解析。
解析
(1)f′(x)=

∴
解得a=2,b=1。
(2)f(x)=2lnx﹣x2,令h(x)=f(x)+m=2lnx﹣x2+m,
则
令h′(x)=0,得x=1(x=﹣1舍去)。
在
当
∴h(x)是增函数;
当x∈[1,e]时,h′(x)<0,
∴h(x)是减函数,
则方程h(x)=0在
即
(3)g(x)=2lnx﹣x2﹣kx,
假设结论成立,则有:
①-②,得

∴
由④得
∴
即

令

则
∴u(t)在0<t<1上增函数,
∴u(t)<u(1)=0,
∴⑤式不成立,与假设矛盾。
∴g'(x0)≠0。
知识点
已知函数

(1)若函数

(2)若方程

正确答案
(1)a=1
(2)
解析
(1)
∵ 
∴ 
∴ 
(2)∵ 

又

即
知识点
若圆






正确答案
解析
圆的圆心为



知识点
已知函数

(1)求实数
(2)设

正确答案
见解析。
解析
解:(1)因为函数


即
即
解得
(2)方法1:由(1)得
所以

所以

因为函数

所以当

即

所以函数

方法2:由(1)得

所以

所以函数

因为函数

所以当

即


所以函数

知识点

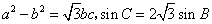
正确答案
解析
略
知识点
在△








正确答案
解析
略
知识点
已知△ABC中,
正确答案
解析
略
知识点
扫码查看完整答案与解析