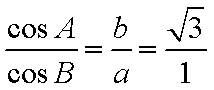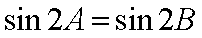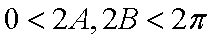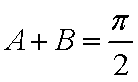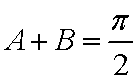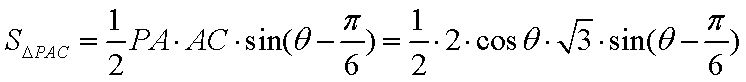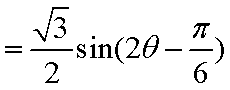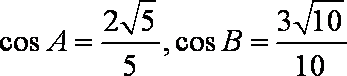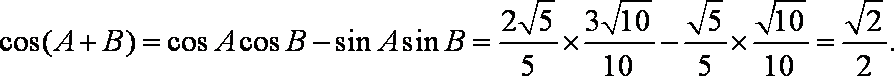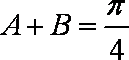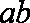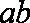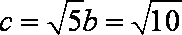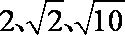- 三角函数与三角恒等变换
- 共3475题
在









(1)求角
(2)若

正确答案
(1)
解析
解析:(1)



又



(2)









知识点
在△








正确答案
见解析
解析
∵


又


在△


三角形面积
知识点
在
(1)求角A的大小;
(2)若


正确答案
见解析。
解析
(1)∵
∴
即

∴
又

(2)
∴
又由余弦定理得
∴

知识点
如图所示,扇形





过点



(1)若


(2)设


正确答案
(1)
解析
解析:
(1)在△

由
得

(2)∵


在△

∴

解法一:记△


∴


解法二:
即

当且仅当
所以




知识点
已知△ABC中,角A、B、C的对边分别
(1)求
(2)求
正确答案
见解析。
解析
(1)
由余弦定理得
(2)由正弦定理知:
知识点
在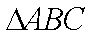
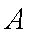
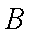
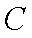
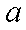
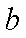

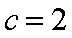
(1)求证: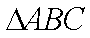
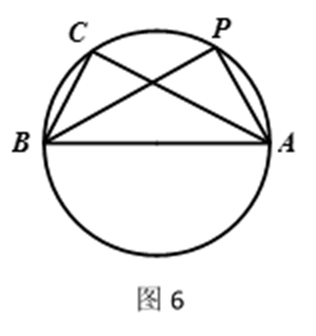
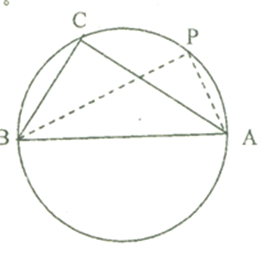
(2)如图6,设圆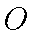
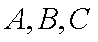
正确答案
见解析
解析
(1)证明:由正弦定理得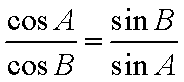
整理为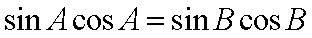
又因为
∴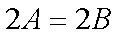
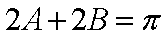
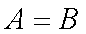
∵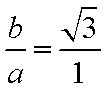
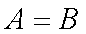
由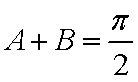
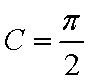
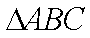
(2)由(1)及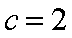
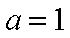
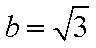
设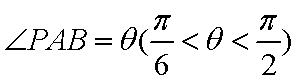
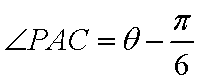
在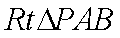
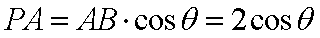
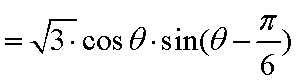
因为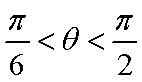
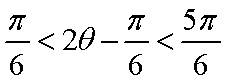
当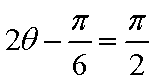
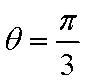
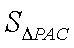
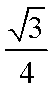
知识点
在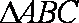
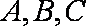
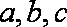
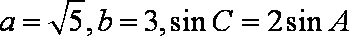
(1)求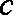
(2)求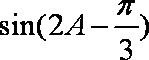
正确答案
见解析
解析
(1)由正弦定理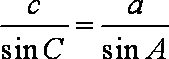
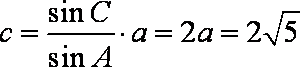

(2)由余弦定理,得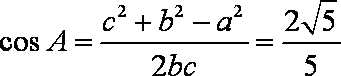

所以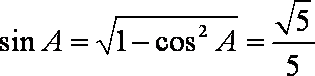
故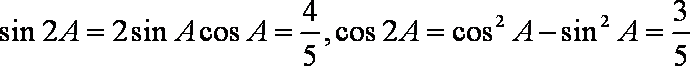
所以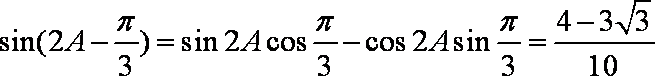
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
在





(1)求角
(2)当

正确答案
见解析
解析
(1)由

由正弦定理得



(2)

由

即


知识点
在△








正确答案
解析
由正弦定理,


知识点
在ABC中,设角A、B、C所对的边分别为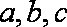
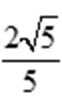
(1)求角C的大小;
(2)若ABC的面积为1,求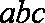
正确答案
(1)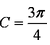
解析
(1)∵
∴ 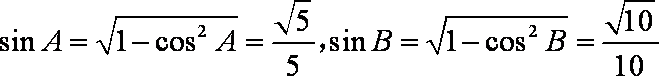
∵ 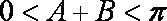
∴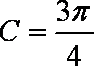
(2)法一:由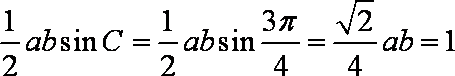
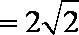
同理得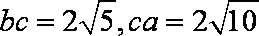
所以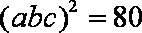
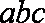
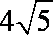
法二:由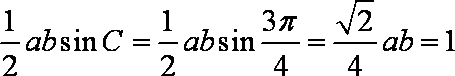

由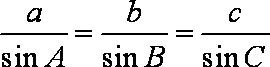
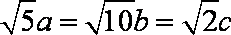
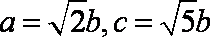
∴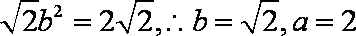
即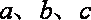
所以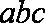
知识点
已知
cosA=

(1)求tanC的值;
(2)若a=

正确答案
见解析
解析
(1)∵cosA=

又
=

整理得:tanC=
(2)由(1)知sinC=
由正弦定理知:

又∵sinB=

∴


知识点
已知在



(1)求角A、B、C的大小;
(2)设函数

正确答案
(1)

解析
解析:(1)由题设及正弦定理知:
∴


当




当


∴

(2) 由(1)及题设知:
当

即

它的相邻两对称轴间的距离为 
知识点
若


(1)求

(2)⊿ABC中a、b、c分别是∠A、∠B、∠C的对边。若

正确答案
(1)
解析
解析:(1)

由题意,函数



所以,

(2)∵(

又因为A为⊿ABC的内角,所以
⊿ABC中, 则由正弦定理得:



知识点
(本小题满分12分)
已知向量



(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1,b=

正确答案
(1)
解析
(1)

因为

(2)由(1)知


由正弦函数图象可知,当



所以
由余弦定理


经检验均符合题意. ……………………10分
从而当



知识点
扫码查看完整答案与解析