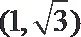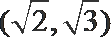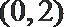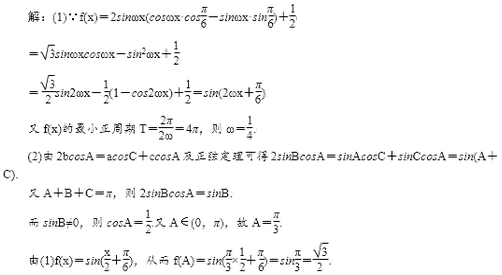- 三角函数与三角恒等变换
- 共3475题
14.在




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.已知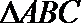
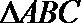
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在







(1)求证:
(2)设圆






正确答案
(1)证明:由正弦定理得

即sin2A=sin2B ∴2A=2B或2A+2B=π,
即A=B或A+B=∵
由A+B=可知c=,∴ΔABC是直角三角形
(2)由(1)及

在RtΔ

所以,




当


解析
解析已在路上飞奔,马上就到!
知识点
3.在△ABC中,若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知










(Ⅰ)若



(Ⅱ)若



正确答案
解(Ⅰ)









解得



(Ⅱ)在







又






解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某观测站C在城A的南偏西

正确答案
解:在


所以
在

所以
由正弦定理

故这时此车距离A城15千米
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC中,a,b,c分别是角A,B,C的对边,若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.△ABC的三个内角A、B、C所对的边分别为a,b,c,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设锐角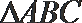
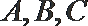
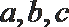
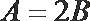
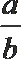
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设


(1)求函数
(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数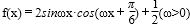
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知a,b,c分别为△ABC三个内角A,B,C的对边,acos C+
(1)求A;
(2)若a=2,△ABC的面积为
正确答案
解:(1)由acos C+
sin Acos C+
因为B=π-A-C,
所以
由于sin C≠0,所以sin

又0<A<π,故A=
(2)△ABC的面积S=

而a2=b2+c2-2bccos A,故b2+c2=8.
解得b=c=2.
解析
解析已在路上飞奔,马上就到!
知识点
19.在



(1)求
(2)求
正确答案
(1)

即:

又在




(2)





解析
解析已在路上飞奔,马上就到!
知识点
17. 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
正确答案
在△BDC中,由余弦定理知cos∠CDB=
sin∠CDB=
∴轮船距港口A还有15海里.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析