- 三角函数与三角恒等变换
- 共3475题
15. 已知在



正确答案
解析
因为



考查方向
解题思路
由正弦定理整理,二倍角正弦公式
易错点
正弦定理的转化
知识点
16.在△ABC中,角A、B、C的对边分别为a、16.在△ABC中,角A、B、C的对边分别为a、b、c,若2ccosB=2a+b,△ABC的面积为S=
正确答案
解析
在
即
再由余弦定理可得,
整理可得
即
考查方向
解题思路
本题主要考查了正余弦定理在解三角形中的应用及诱导公式和两角和的正弦公式、基本不

易错点
本题在化边为角的过程中易错
知识点
17.在




(1)求角B的大小;
(2)若等差数列





正确答案
(1)
(2)
解析
试题分析:本题第(1)问属于解三角形以及三角恒等变换的知识,是基础知识,难度中等;第(2)问是数列求和的问题,用主要考查了裂项相消法求数列的前n项和,解答过程如下:
(Ⅰ)由









解得
(Ⅱ)设



∴
又



∴

考查方向
解题思路
1、第(1)问根据余弦定理求出
2、第(2)问可以先用已知条件求出
易错点
本题容易因为忽略三角形内角的范围而导致错误的出现。
知识点
14.在Rt△ABC中,∠A=90°,AB=AC=2,点D为AC中点,点E满足

正确答案
-2
解析


所以
考查方向
本题主要考查向量的线性运算、平面向量基本定理以及向量的数量积等知识,意在考查考生的运算能力和逻辑推理能力。
解题思路
1.先将向量

2.利用数量积运算求出所求答案。
易错点
1.不会将所求的向量都用基底表示出来;
2.向量的数量积运算律和实数的运算混淆。
知识点
7.在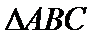
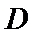
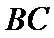
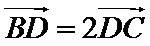

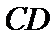
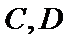
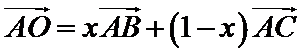
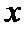
正确答案
解析
如图,由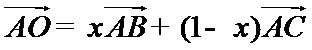
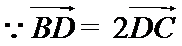
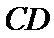

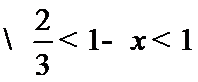
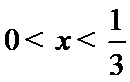
A选项不正确,B选项不正确,D选项不正确,所有选C选项.
考查方向
解题思路
1、通过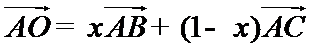
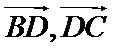
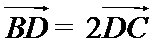
A选项不正确,B选项不正确,D选项不正确,所有选C选项.
易错点
1、本题易在平面向量的加法和减法的运算规律上出错,将二者的运算法则混淆. 2、本题不容易找出各向量之间的联系,从而使题解无法进行.
知识点
15.在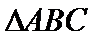
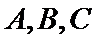
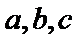
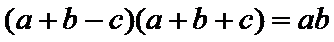
(1)求角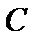
(2)若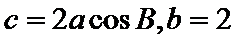
正确答案
(1)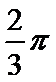
(2)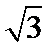
解析
试题分析:本题属于解三角形中的基本问题,难度不大。
(1)此类问题主要应用正(余)弦定理和三角形面积公式;
(2)注意边和角的统一。
解析:(1)在△ABC中,由(a+b-c)(a+b+c)=ab,得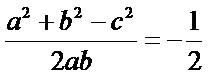
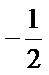
因为0<C<π,所以C=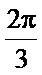
(2)因为c=2acosB,由正弦定理,得
sinC=2sinAcosB,
因为A+B+C=π,所以sinC=sin(A+B),
所以sin(A
又-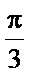
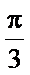
所以A-B=0,即A=B,所以a=b=2.
所以△ABC的面积为S△ABC=absinC=×2×2×sin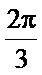
考查方向
本题旨在考查三角函数的基本关系、正弦定理、余弦定理、三角形面积公式、向量的数量积等基本知识,考查运算求解能力.难度较小.
解题思路
本题旨在考查三角函数的基本关系、正弦定理、余弦定理、三角形面积公式、向量的数量积等基本知识.
解题步骤如下:
化简已知条件,利用余弦定理求解。
边角互化,利用正(余)弦定理和三角形面积公式求解。
易错点
第一问中化简易出错误。
第二问不知道统一成边或者角进行处理。
知识点
9.在△ABC中,内角A,B,C 所对的边分别为 a,b,c,若 cos 2B+cosB=1-cos AcosC 则( )
正确答案
解析
由cos 2B+cosB=1-cos AcosC
得到sin 2B=cos Acos C-cos(A+C)
所以sin 2B=cos Acos C-cos AcosC+sinAsinC
所以sin 2B=sinAsinC
由正弦定理得,b2 = ac,所以a,b,c 成等比数列,故选B。
考查方向
解题思路
1.先利用三角函数中的公式将cos 2B+cosB=1-cos AcosC化简;
2.利用正弦定理得到边之间的关系即可。
易错点
1.对于题中cos 2B+cosB=1-cos AcosC的化简不会入手;
2.对于三角函数的化简出错
知识点
正确答案
知识点
3.在△ABC中,角A,B,C所对的边分别为a,b,c,若

正确答案
解析

考查方向
本题主要考查解三角形的正弦定理
解题思路
利用正弦定理求解,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代换时发生错误。
知识点
8.在






正确答案
解析
由题意,得
即
由正弦定理,
得
整理,
得

所以联立以上两式可得b=2.
故选择C选项。
考查方向
解题思路
利用两角和与差的正弦及余弦定理即可求出b值。
易错点
对相关知识不熟悉导致出错。
知识点
17.△ABC的内角A,B,C的对边分别别为a,b,c,已知
(I)求C;
(II)若

正确答案
解(Ⅰ)∵2cos C(acosB+bcosA)=C
∴2cos C(sinAcos B+sinBcosA)=sinC
∴2cosC sin(A+B)=sinC
∴2cosC sinC=sin C
∴ 0<C<π
∴ cosC= 
∴ C= 
(Ⅱ) ∵△ABC面积为
∴
∴(a+b)2=a2+b2+2ab=13+12=25
∵a+b=5
∴a+b+c=5+
∴
知识点
(5分)(2015•上海)已知点A的坐标为(4

正确答案
知识点
(14分)(2015•上海)如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
(1)求t1与f(t1)的值;
(2)已知警员的对讲机的有效通话距离是3千米.当t1≤t≤1时,求f(t)的表达式,并判断f(t)在[t1,1]上的最大值是否超过3?说明理由.
正确答案
解:(1)由题意可得t1=

设此时甲运动到点P,则AP=v甲t1=5×

∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t)=PQ=
=
=
当
∴f(t)=PB=AB﹣AP=5﹣5t
∴f(t)=
∴当

故f(t)的最大值超过了3千米.
知识点
22.如图,在









(1)求证:
(2)求线段
正确答案
(1)见解析;
(2)
解析
试题分析:本题属于圆的知识的综合应用问题,属于简单题,解析如下:
(1)证明:由已知∠BDC=∠BEC=90°,
所以B,C,D,E四点在以BC为直径的圆上,
由割线定理知:
(2)解:如图,过点F作FG⊥BC于点G,
由已知,∠BDC=90°,又因为FG⊥BC,所以B,G,F,D四点共圆,
所以由割线定理知:
同理,F,G,C,E四点共圆,由割线定理知:

①+②得:
即
所以
考查方向
解题思路
(1)由已知条件B、C、D、E四点在以BC为直径的袁尚,从而由割线定理即可使问题得证;
(2)过点F做
易错点
相关知识点不熟容易证错。
知识点
(2015•上海)在锐角三角形 A BC中,tanA=


正确答案
知识点
扫码查看完整答案与解析