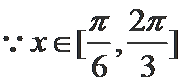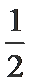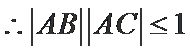- 三角函数与三角恒等变换
- 共3475题
在教育宗旨问题上,梁启超主张通过教育培养
A.政治家
B.学术人才
C.新国民
D.实业人才
正确答案
C
解析
[分析] 本题旨在考查考生对中国近代维新派教育家及其代表人物教育思想贡献及其历史意义的掌握程度。维新派教育家的思想贡献在于首先明确提出普及教育的主张和培养具有时代人格精神的国民,这是他们区别于洋务派教育思想之处。尽管他们不排斥培养政治家、学术人才和实业人才,但其着眼点显然不在于此。故本题正确答案为C。
已知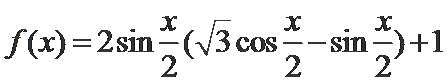
17.若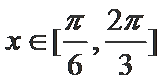
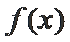

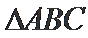
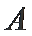
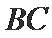
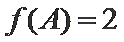
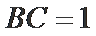
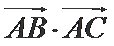
正确答案
(1)值域为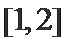
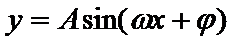
解析
(Ⅰ)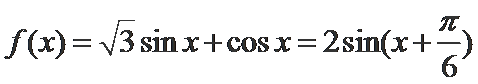

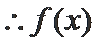
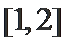
解题思路
利用降幂公式、辅助角公式把函数化成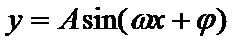
利用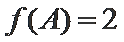
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
正确答案
最大值为
解析
(Ⅱ)
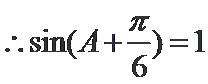
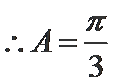
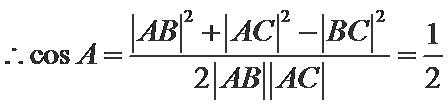
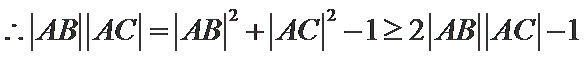
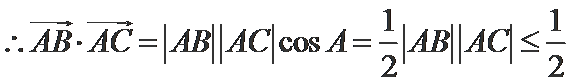
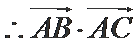
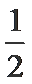
考查方向
解题思路
利用降幂公式、辅助角公式把函数化成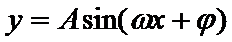
利用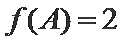
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
在△ABC中,已知AB=2,AC=3,A=60°.
17.求BC的长;
18.求sin2C的值.
正确答案
解析
(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+8﹣2×2×3×
所以BC=
考查方向
解题思路
直接利用余弦定理求解即可。
易错点
本题考查余弦定理的应用,正弦定理的应用,在计算时易错。
正确答案
解析
由正弦定理可得:



∵AB<BC,∴C为锐角,
则cosC=


因此sin2C=2sinCcosC=2×

考查方向
解题思路
利用正弦定理求出C的正弦函数值,然后利用二倍角公式求解即可.
易错点
本题考查二倍角的三角函数,在限制角的范围过程中易错。
16.在


正确答案
知识点
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是
正确答案
8
知识点
16.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知

(1)求tanC的值;
(2)若△ABC的面积为7,求b的值。
正确答案
(1)2;(2)b=3;
解析
试题分析:根据正弦定理可将条件中的边之间的关系转化为角之间的关系,再将式子作三角恒等变型即可求解;(2)根据条件首先求得
(1)由






(2)由



又∵


又∵


考查方向
解题思路
(1)利用正弦定理和三角函数的诱导公式,同角三角函数的关系式进行化简
求解;(2)求出角C的正弦和余弦值,再求出sinB,由正弦定理求出c,最后利用三角形的面
积求出b的值.
易错点
注意三角函数中公式的应用.
知识点
在



17.求角
18.设函数



正确答案
详见解析
解析
解:(Ⅰ)在

由余弦定理可得
∵

考查方向
余弦定理
解题思路
利用余弦定理求cosA的值,进而求出A的大小
易错点
判断角A的值时,要考虑A的取值范围
教师点评
运用余弦定理求角大小时,要注意考虑角的范围
正确答案
详见解析
解析
(Ⅱ)


∵

∴
考查方向
三角函数的等价变形,三角函数的化简求值 正弦定理
解题思路
先化简成同名同角函数,然后利用正弦定理求边长
教师点评
此类问题常考察对三角函数恒等变形的掌握,要注意牢记各类三角函数恒等变形公式。
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是 。
正确答案
8
知识点
16.在


正确答案
解析



所以
考查方向
解三角形,正弦定理
解题思路
先求出sinA和sinC的表达式,然后由正弦定理得到sinB的值
易错点
三角函数相关公式掌握不牢固
知识点
12. 在




则
正确答案
解析

由正弦定理知,
所以
考查方向
余弦定理.正弦定理的应用
解题思路
已知等式左边利用平方差公式化简,再利用完全平方公式展开,再利用余弦定理表示出cosA,将得出的关系式代入求出cosA的值,由A的三角形的内角,利用特殊角的三角函数值即可求出A的度数.再利用正弦定理求出b的值
易错点
计算化简能力弱
知识点
在△ABC中,内角A,B,C所对的边分别为a,b,c,且2sin(A-B)=asinA-bsinB,a≠b.
16.求边c;
17.若△ABC的面积为1,且tanC=2,求a+b的值.
正确答案
详见解析
解析
考查方向
解三角形,正弦定理和余弦定理的应用
解题思路
根据正弦定理求出a b之间的关系,用余弦定理求出C的值
易错点
对正弦定理、余弦定理的性质掌握不好
正确答案
详见解析
解析
考查方向
正弦定理、余弦定理的性质和应用
解题思路
根据余弦定理求出cosC的值,然后利用所给条件,求出a+b的值
根据公司法律制度的规定,股份有限公司的财务会计报告应在召开股东大会年会的一定期间以前置备于公司,供股东查阅。该期间为( )。
A.10日
B.15日
C.20日
D.25日
正确答案
C
解析
根据公司法律制度的规定,股份有限公司的财务会计报告应在股东大会年会召开前20日置备于公司,供股东查阅。
17.








(1)求
(2)若


正确答案
(1)因为

由正弦定理,得
又

由于
(2)解法一:由余弦定理,得
而
得
因为

故

解法二:又正弦定理,得
从而
又由


故
所以

解析
解析已在路上飞奔,马上就到!
知识点
解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)







(Ⅰ) 求
(Ⅱ)若



正确答案
(Ⅰ)


(Ⅱ)因为








解析
解析已在路上飞奔,马上就到!
知识点
已知函数



正确答案
解析
离开家LKS酒店离开加大啊大大大
考查方向
卡结算点开链接阿斯利康的
解题思路
爱是顶顶顶顶顶的顶顶顶顶顶多多多
易错点
是事实上事实上事实上事实上是
教师点评
阿萨的顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶大多多多立刻就撒了肯德基萨拉快点进来看三就了看撒娇的了卡萨就离开的就款了撒娇的理科生就看到了奖励卡检索到立刻就撒了肯德基来看撒娇的离开家萨克雷的就来看撒娇的理科生都流口水了肯定是考虑到看拉手机登了卡结算了肯德基撒立即克拉拉肯德基凯撒蓝就点开了升级打开老师教的款了撒娇的理科生就看到了上考虑绝对是理科开水将打开实际空间萨克的垃圾筐的撒空间的卡卡的萨拉大乐扣乐扣
知识点
扫码查看完整答案与解析