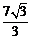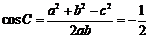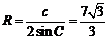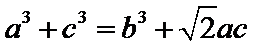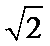- 三角函数与三角恒等变换
- 共3475题
5.底面边长为2m,高为1m的正三棱锥的全面积为( )m2
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
4.已知f(x)是定义在R上的可导函数,f'(x)为f(x)的导函数,又有两个向量m=(f(x),-1),n=(1,f'(x)),且对于x∈R,两向量m,n的夹角范围都是[0,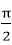
正确答案
解析
因为向量m,n的夹角范围都是[0,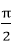
所以m·n=(f(x),-1)·(1,f'(x))=f(x)-f'(x)>0,
令F(x)=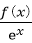
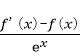
所以F(x)=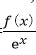
所以F(2015)<F(0),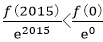
F(-2014)>F(0),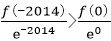
知识点
7.某船在海平面








正确答案
解析
由题可知,AB=6,AC=8.1,A=30o,可求得BC=
考查方向
本题主要考查了解三角形的实际应用举例。
解题思路
本题考查余弦定理,解题步骤如下:利用余弦定理求解。
易错点
本题要注意余弦定理。
知识点
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
21.节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形














(1)将

(2)试确定
正确答案
(1)

(2)点





解析
(1)由已知得
即

(2)记


解得

由于







考查方向
本题以实际问题为背景,主要考查函数解析式的构建以及函数最值的求解,考查数学建模的能力,是中档题.以实际问题为背景的生活中的优化问题,这类问题在近几年各省市的高考试卷中频频出现,是高考的热点问题.这类问题往往涉及到建立函数关系式和函数的最值,一般先设自变量、因变量,建立函数关系式,并确定其定义域,求最值时可利用三角函数的有界性、函数的单调性,也可直接利用导数求最值,要掌握求最值的方法和技巧.也注意结果应与实际情况相符合.
解题思路
先建立函数,再利用三角函数的有界性求
易错点
建立函数过程中,容易遗忘定义域,还要注意实际情况;求最值的有多种方法,还要注意结果应与实际情况相符合.
知识点
9. 在△ABC中,AB=AC,M为AC的中点,BM=
正确答案
解析
如图,设等腰三角形顶角为


所以当

考查方向
解题思路
如图,
设等腰三角形顶角为


易错点
不能选取合适的变量建立函数模型,或在复杂计算过程中出错
知识点
21.如图,在一条景观道的一端有一个半径为







(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱



(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带



正确答案
(1)
(2)94米.
解析
(1)

∴

过点


则

∴
∴
答:望远镜的仰角
(2)在

∴
∴

∴
答:绿化带的长度为94米.
考查方向
本题主要考查利用正弦定理解三角形,是一道有实际问题背景的应用题.应用题的考查在近几年的各省高考题中出现的频率非常高,通常与函数、不等式、三角、数列、解析几何、立体几何、向量、概率统计等知识点相结合进行命题,是高考的热点问题.
解题思路
题(1),摩天轮做匀速转动,逆时针15分钟转一圈,可得5分钟转过120°,过点C作CH⊥AB于点H,解三角形可得望远镜的仰角
(2)由题意可求CD,利用正弦定理即可解得BD的长度.
易错点
面对题设条件,无法确定什么时候用正弦定理什么时候用余弦定理或其它相关知识求解三角形的边与角.
知识点
14.已知




(i) 在满足下述条件的三角形中,存在“友好”三角形的是____:(请写出符合要求的条件的序号)
①
②
③
(ii) 若等腰
正确答案
②;
解析







考查方向
本题主要考察了解三角形问题,属于难题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单解三角形的问题。
易错点
本题易在公式变形时发生错误,导致题目出错。
知识点
16.如图所示,已知








正确答案
解析
本题已知直角



考查方向
解三角形.
解题思路
利用解直角三角形相关公式求解
易错点
分析试题,找不到解决问题的突破口。
知识点
7


正确答案
解析




考查方向
本题主要考查解三角形
解题思路
利用两角和与差的正弦、余弦函数公式化简,根据正弦、余弦函数求出cos(A+B)与sin(A+B)的值,进而求出A,B,C的度数,利用正弦定理化简所求的式子,计算即可得到结果
易错点
利用正余弦定理边角互化
知识点
9. 已知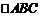
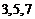
正确答案
解析
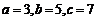
∴
∴
知识点
15. 在
(I)求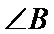
(II)求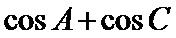
正确答案
知识点
21.如图,在一条景观道的一端有一个半径为







(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱



(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带



正确答案
(1)
(2)94米
解析
(1)



过点




答:望远镜的仰角
(2)在

由正弦定理得:
答:绿化带的长度为94米.
考查方向
解题思路
本题考查了角的概念,反三角函数和正弦定理的基本知识和解题能力,数形结合,合理转换边角关系即可得解。
易错点
本题必须注意边角关系的合理转换,忽视则会出现错误。
知识点
16.








正确答案
解析
由题意






考查方向
解题思路
利用交平分线的性质求AC,再利用向量及余弦定理即可求AD。
易错点
对相关知识点的不熟悉导致错误。
知识点
在


正确答案
考查方向
易错点
1、本题在把题意转化成余弦定理模型上易出错。
知识点
扫码查看完整答案与解析