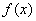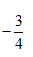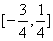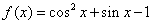- 三角函数与三角恒等变换
- 共3475题
如图,












22. 求

23. 已知警员的对讲机的有效通话距离是3千米.当



正确答案
(1)

解析
试题分析: (1)由题意可得

(1)


所以

考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
实际问题数学模型的转化
正确答案
(2)超过了3千米.
解析
试题分析: (2) 分段求出对应函数解析式,根据函数单调性求得最值即可.
(2)当



所以

所以

当


所以
所以
所以当 


考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
分段函数单调性最值的求解


17.求角B的大小;
18.若BD为AC边上的中线,

正确答案
见解析
解析









考查方向
解题思路
利用正弦定理求角度
易错点
正弦定理、余弦定理的性质掌握不好
正确答案
见解析
解析
法一:在三角形









法二: 延长













考查方向
解题思路
用余弦定理求面积
易错点
正弦定理、余弦定理的性质掌握不好
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
13.海轮“和谐号”从A处以每小时21海里的速度出发,海轮“奋斗号”在A处北偏东

正确答案
解析
由题意做出平面图,如图所示,





考查方向
解题思路
1)根据题意,以及方向角,画出平面图形;
2)在
易错点
本题应当根据题意画出准确的图像,学生容易画错,计算也是 比较难的;
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为________。
正确答案
1
解析
函数f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cos φ-cos(x+φ)sin φ=sin x,故其最大值为1.
知识点
已知函数
(1)求函数

(2)若

正确答案
见解析。
解析
(1)解:由
所以函数
因为





(2)解:由(1)可知
又因为
由
从而
所以
知识点
函数
正确答案
解析


=

当


知识点
设函数

(1)若


(2)若




正确答案
见解析。
解析
(1)
当

而


此时



∴


(2)依题意


整理,得
又


而





知识点
13.如图,一辆汽车在一条水平的公路上向正西行驶,到





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设向量
(1)若

(2)设函数
正确答案
见解析
解析
知识点
已知函数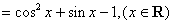
(1)求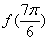
(2)当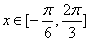
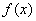
正确答案
(1)
(2)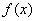
解析
(1)因为
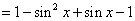
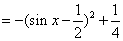
所以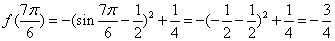
(或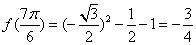
(2)因为
所以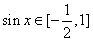
所以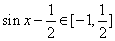
所以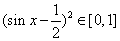
所以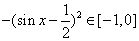
所以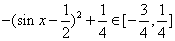
所以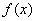
知识点
对于函数
正确答案
解析
略
知识点
设函数


正确答案
解析
略
知识点
设





(1)求实数

(2)
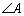




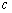



正确答案
见解析。
解析
(1)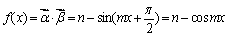
因为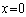
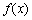
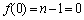
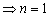
易知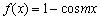

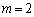

(2)由(Ⅰ)可知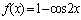
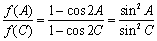
由正弦定理及余弦定理有: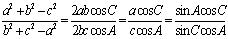
故
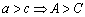
于是
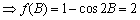
知识点
扫码查看完整答案与解析