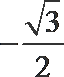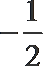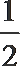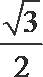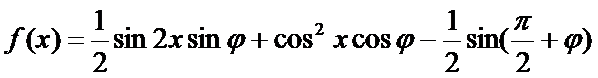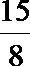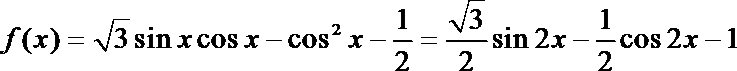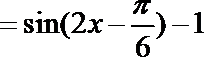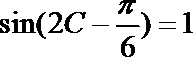- 三角函数与三角恒等变换
- 共3475题
11.函数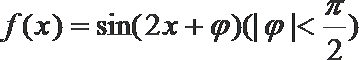
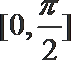
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.等腰





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数
(Ⅰ)求函数


(Ⅱ)已知




正确答案
(Ⅰ)

∴函数




故

(Ⅱ)由题意,



在

由


∴当

解析
解析已在路上飞奔,马上就到!
知识点
12.给定两个长度为1的平面向量






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数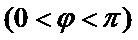
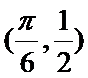
(1) 求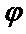
(2)将函数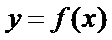
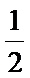
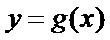
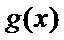
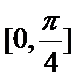
正确答案
(1)将已知函数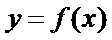
整理化简为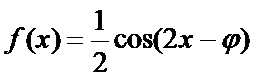
因其图象过点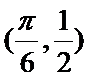
可得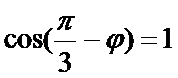
又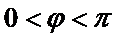
所以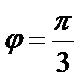
(2)由(1)知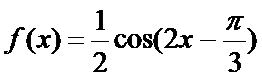
将函数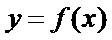
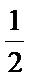
纵坐标不变,得到函数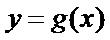
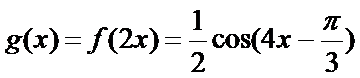
因为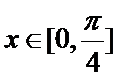
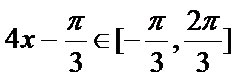
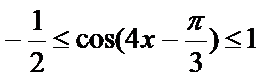
所以
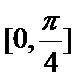
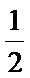
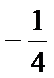
解析
解析已在路上飞奔,马上就到!
知识点
7.函数f(x)=sinωx+acosωx(ω>0)的图象关于M(

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ ABC的三个内角A、B、C所对的边分别a、b、c,
(Ⅰ)求角C的大小;
(Ⅱ)当

正确答案
(Ⅰ)因为

因为


又因为


(Ⅱ)由(Ⅰ)知,
所以
=

因为

所以

解析
解析已在路上飞奔,马上就到!
知识点
3.对于函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数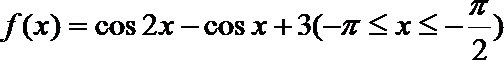
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(Ⅰ)求函数

(Ⅱ)求

正确答案
解:(Ⅰ)
(Ⅱ)
所以,
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数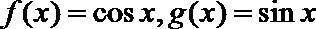
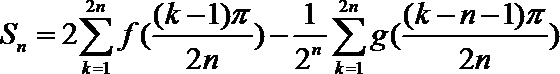
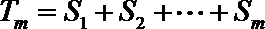



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)当

(2)已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
21. 如下图,某小区准备绿化一块直径为










(1)试用



(2)若

正确答案
(1)在

设正方形的边长为

由

所以
(2)
令


所以

所以函数

因此当


所以当
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数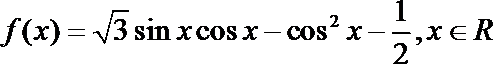
(1) 求函数
(2)已知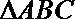
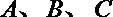
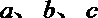
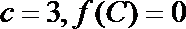
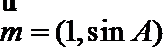
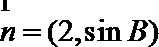
正确答案
(1)
∴ 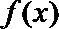
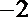


(2)∵ 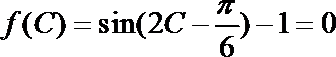
∵ 
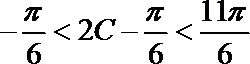

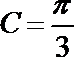
∵ 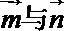
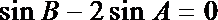
由正弦定理 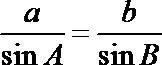
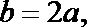
∵ 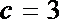
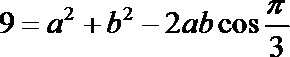
解方程组①②,得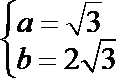
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析