- 三角函数与三角恒等变换
- 共3475题
14.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在

(I)求角C的大小;
(II)若


正确答案
(I)由2ccosA=2b﹣
利用正弦定理化简得:2sinCcosA=2sinB﹣
即2sinCcosA=2sin(A+C)﹣
整理得:
2sinCcosA=2sinAcosC+2cosAsinC﹣
即sinA(2cosC﹣
∵sinA≠0,
∴2cosC﹣

则C=
解析
解析已在路上飞奔,马上就到!
知识点
1.sin2100 = ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设
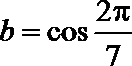
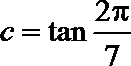
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知A,B,C是


(I)求角A;
(II)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知sinθ=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数y = 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知



正确答案
arcsin
解析
解析已在路上飞奔,马上就到!
知识点
21.已知
求:(1)
(2)
正确答案
由已知得cos(

∴tan(

即tan
(1)
(2)




解析
解析已在路上飞奔,马上就到!
知识点
23.已知



正确答案
由tanβ=-
得β∈(
由tanα=tan[(α-β)+β]=
α∈(0,π)
∴ 0<α<
∴ 0<2α<π
由tan2α=
∴ 知0<2α<
∵ tan(2α-β)=
由①②知 2α-β∈(-π,0)
∴ 2α-β=-
解析
解析已在路上飞奔,马上就到!
知识点
14.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设





正确答案
原函数变形为
y=-
∵-1≤sinx≤1,a≥0
∴若0≤a≤2,当sinx=-
ymax=1+b+
当sinx=1时,ymin=-
=-a+b=-4 ②
联立①②式解得a=2,b=-2
y取得最大、小值时的x值分别为:
x=2kπ-

若a>2时,
∴ymax=-
ymin=-
由③④得a=2时,而
故只有一组解a=2,b=-2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析