- 三角函数与三角恒等变换
- 共3475题
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在△






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设锐角三角形

(1)求B的大小;
(2)求
正确答案
(1)由

所以
由△ABC为锐角三角形得B=
(2)
=
由△ABC为锐角三角形知,

所以,

由此有
所以,

解析
解析已在路上飞奔,马上就到!
知识点
6. 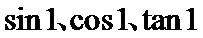
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.求值:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知







正确答案

解析
解析已在路上飞奔,马上就到!
知识点
17.已知⊿ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:
(1) 2sinBcosC-sin(B-C)的值;
(2)若a=2,求⊿ABC周长的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,两块斜边长相等的直角三角板拼在一起,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图,已知









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
6.类似于十进制中逢10进1,十二进制的进位原则是逢12进1,采用数字0,1,2…,9和字母M、N共12个计数符号,这些符号与十进制数的对应关系如下表:
例如,由于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,在三棱锥















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四棱锥




(Ⅰ)求证:
(Ⅱ)求二面角
(Ⅲ)线段



正确答案
解法一:
(Ⅰ)因为



因为



在


由根据三垂线定理可得知:
(Ⅱ)设






作


所以

由已知得,

所以

所以二面角

(Ⅲ)当



证明:取




所以


所以

又


解法二:以D为原点,以DA、DC、DP为x轴、y轴、z轴建立空间直角坐标系,
则



(Ⅰ)

所以
所以
(Ⅱ)






设平面



所以


(Ⅲ)令
由已知,



即


所以 当



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析