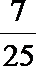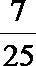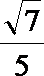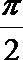- 三角函数与三角恒等变换
- 共3475题
5.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在边长为1的正三角形ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.
(1)求

(2)在

正确答案
(1)由于f(x)=sinx(1+sinx)+cos2x=1+sinx
当x∈

故 
故函数f(x)在

(2)在△ABC中,由
可得sinA=
所以sinC=sin(A+B)
=sinAcosB+cosAsinB
=

故f(C)=1+sinC=1+
解析
解析已在路上飞奔,马上就到!
知识点
18.在平面直角坐标系中,锐角

(1)如果A、B两点纵坐标分别为
(2)在(1)条件下,求
(3)已知

正确答案
(1)根据三角函数的定义
得
又α是锐角,所以,
(2)由(1)知,
又α是锐角,β是钝角
所以
所以
(3)由题意可知,
所以
因为
所以
所以函数
解析
解析已在路上飞奔,马上就到!
知识点
19.在四棱锥





(1)求证:
(2)求二面角
正确答案
(1)在四棱锥P﹣ABCD中,
由于E为PB的中点,
再取DP的中点F,AP的中点为K,
则FK是三角形PAD的中位线,
FK平行且等于
EF是三角形PBD的中位线,
故有BD∥EF ①.
再根据PA=PB=AD=AB=4BC=4,
AD∥BC,且AD⊥面PAB,
可得EF=



FC=


显然有 CE2+EF2=FC2,
∴ EF⊥CE ②.
由①、②可得BD⊥CE.
(2)由题意可得平面ABCD⊥平面PAB,
过点E作EG⊥AB,G为垂足,则EG⊥平面ABCD.
再过点G作GH⊥AC,H为垂足,则有三垂线定理可得,
EH⊥AC,
∴ ∠EHG为二面角E﹣AC﹣B的平面角.
由

可得

解得 EG=
由于AD⊥面PAB,AD∥BC,
∴ BC⊥面PAB,∴ CPB⊥面PAB.
再根据等边三角形种AE⊥PB,
∴ AE⊥平面PBC,∴AE⊥EC.
再根据

可得 

解得 EH=2
直角三角形EGH中,sin∠EHG=

∴ cos∠EHG=

即二面角E﹣AC﹣B的余弦值为 
解析
解析已在路上飞奔,马上就到!
知识点
22.
(1)若

(2)若


(3)当

正确答案
(1)


因为x=2为f(x)的极值点,所以f'(2)=0.
即
又当a=0时,f'(x)=x(x﹣2),
从而x=2为f(x)的极值点成立.
(2)因为f(x)在区间[3,+∞)上为增函数,
所以
在区间[3,+∞)上恒成立.
①当a=0时,f'(x)=x(x﹣2)≥0在[3,+∞)上恒成立,
所以fx)在[3,+∞上为增函数,故a=0符合题意.
②当a≠0时,由函数f(x)的定义域可知,
必须有2ax+1>0对x≥3恒成立,故只能a>0,
所以2ax2+(1﹣4a)x﹣(4a2+2)≥0对x∈[3,+∞0上恒成立.
令g(x)=2ax2+(1﹣4a)x﹣(4a2+2),其对称轴为
因为a>0所以
从而g(x)≥0在[3,+∞)上恒成立,
只要g(3)≥0即可,
因为g(3)=﹣4a2+6a+1≥0,
解得
因为a>0,所以
综上所述,a的取值范围为
(3)若
方程


问题转化为
b=xlnx﹣x(1﹣x)2+x(1﹣x)=xlnx+x2﹣x3在(0,+∞)上有解,
即求函数g(x)=xlnx+x2﹣x3的值域.
以下给出两种求函数g(x)值域的方法:
方法1:因为g(x)=x(lnx+x﹣x2),
令h(x)=lnx+x﹣x2(x>0),
则
所以当0<x<1,h′(x)>0,
从而h(x)在(0,1)上为增函数,
当x>1,h′(x)<0,
从而h(x')在(1,+∞上为减函数,
因此h(x)≤h(1)=0.
而,故b=x•h(x)≤0,
因此当x=1时,b取得最大值0.
方法2:因为g(x)=x(lnx+x﹣x2),
所以g'(x)=lnx+1+2x﹣3x2.
设p(x)=lnx+1+2x﹣3x2,
则
当
所以p(x)在
当
所以p(x)在
因为p(1)=0,故必有
又
因此必存在实数
使得g'(x0)=0,
∴当0<x<x0时,g′(x)<0,
所以g(x)在(0,x0)上单调递减;
当x0<x<1,g′(x)>0,
所以,g(x)在(1,+∞)上单调递减;
又因为
当x→0时,lnx+
则g(x)<0,又g(1)=0.
因此当x=1时,b取得最大值0.
解析
解析已在路上飞奔,马上就到!
知识点
6.若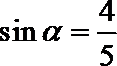

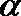
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数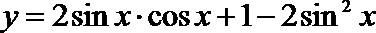
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.设


正确答案

原式
解析
解析已在路上飞奔,马上就到!
知识点
5. 使函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析