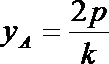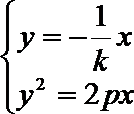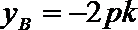三角函数与三角恒等变换
共3475题

三角函数与三角恒等变换
共3475题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10．下面使用类比推理正确的是（）

A“若，则”类推出“若，则”

B“若”类推出“”

C“若” 类推出“ （c≠0）”

D“” 类推出“”

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

简答题 · 12 分

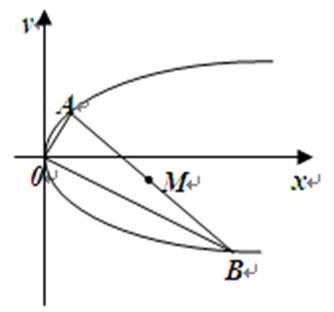
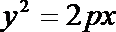
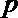
19．如图，过抛物线（为常数＞0）的顶点作两条互相垂直的弦OA、OB。

（1）设OA的斜率为k，试用k表示点A、B的坐标；

（2）求弦AB中点M的轨迹方程。

正确答案

（1）∵ 依题意可知直线OA的斜率存在且不为0

∴ 设直线OA的方程为（）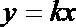

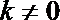
∴ 联立方程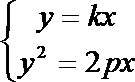

解得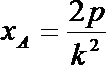

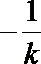
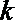
以代上式中的，

解方程组

解得

∴ A（，），B（，）。

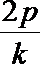
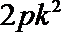
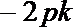
（2）设AB中点M（x，y），

则由中点坐标公式，

得

消去参数k，

得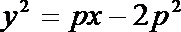

即为M点轨迹的普通方程。

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

7．若，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

7．为圆内异于圆心的点，则直线与该圆的位置关系为（）

A相切

B相交

C相离

D相切或相交

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

2. 若，则点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

11．设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则；类比这个结论可知：四面体S－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为R，四面体P－ABC的体积为V，则R＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

2．如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE，BE，∠APE的平分线分别与AE、BE相交于C、D，若∠AEB=，则∠PCE等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

15．根据以下各组条件解三角形，解不唯一的是（）

A，，

B，，．

C，，．

D，，．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

8. 在△中，若，则△是( )

A等边三角形

B锐角三角形

C钝角三角形

D直角三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

10. 已知△ABC为等边三角形,,设点P,Q满足,,,若,则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

简答题 · 12 分

20.在△ ABC中，角A,B,C的对边分别为a，b，c，已知

（1）求的值。

（2）若，求△ABC的面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

7.在中，若，则的形状是（）

A直角三角形

B等边三角形

C不能确定

D等腰三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

简答题 · 12 分

18.已知为锐角的三个内角，向量,

，且．

（Ⅰ）求的大小；

（Ⅱ）求取最大值时角的大小．

正确答案

（Ⅱ）是锐角三角形，且，

当取最大值时，即．

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

10.在直角梯形ABCD中，，动点在以点为圆心，且与直线相切的圆内运动，设，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

填空题 · 4 分

3．已知角的终边上的一点的坐标为，则角的最小正值为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 平面向量

百度题库 > 高考 > 理科数学 > 三角函数与三角恒等变换

扫码查看完整答案与解析