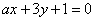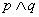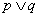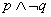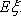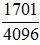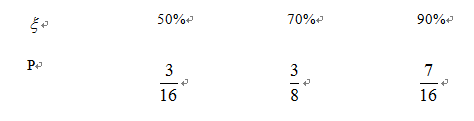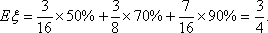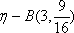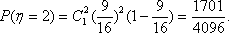两条直线平行的判定
共15题

· 两条直线平行的判定

两条直线平行的判定
共15题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

9．在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，若a、b、c成等差数列，sinB= 且△ABC的面积为，则b= _________ ．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线平行的判定

题型：单选题

单选题 · 5 分

设aR，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x＋(a＋1)y＋4＝0平行”的

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

当a＝1时，直线l1：x＋2y－1＝0与直线l2：x＋2y＋4＝0显然平行；若直线l1与直线l2平行，则有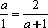：，解之得：a＝1 or a＝﹣2.所以为充分不必要条件。

知识点

充要条件的判定两条直线平行的判定

题型：单选题

单选题 · 5 分

给出命题p：直线互相平行的充要条件是；命题q：若恒成立，则.关于以上两个命题，下列结论正确的是（）

A命题“”为真

B命题“”为假

C命题“”为真

D命题“”为真

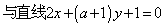
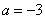
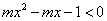
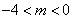
正确答案

解析

略

知识点

充要条件的判定含有逻辑联结词命题的真假判断不等式恒成立问题两条直线平行的判定

题型：简答题

简答题 · 16 分

已知直线为曲线在点处的一条切线。

（1）求a，b的值；

（2）若函数的图象与函数（n＞0）的图象交于，

两点，其中＜，过PQ的中点R作轴的垂线分别交，于点M、N，

设C1在点M处的切线的斜率为，C2在点N处的切线的斜率为，求证：＜。

正确答案

见解析

解析

解：（1）直线的斜率为1，且过点，

又，∴∴，；

（2）的中点为，

∴，

，

由，∴，则，

则

，

又，

法一：令，＞1，则，

因为＞1时，＞0，所以在上单调递增，故＞，

则＞。

法二：令，＞1，，

因为，所以＞1时，＞０，

故在上单调递增，从而＞０，即，

于是在上单调递增，

故＞即＞，＞，则＞

知识点

两条直线平行的判定

题型：单选题

单选题 · 5 分

在中，=90°AC=4，则等于

A-16

B-8

D16

正确答案

解析

本题考查了向量数量积的定义运算。,故选D.

知识点

两条直线平行的判定

题型：简答题

简答题 · 14 分

如图，一个小球从M处投入，通过管道自上面下落到A或B或C，已知小球从每个叉口落入左右两个管道的可能性是相等的。某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为1，2，3等奖.

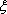
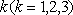
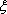
（1）已知获得1，2，3等奖的折扣率分别为50%，70%，90%，记随机变量为获得等奖的折扣率，求随机变量的分布列及数学期望

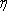
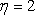
（2）若有3人次（投入1球为1人次）参加促销活动，记随机变量为获得1等奖或2等奖的人次，求P（）.

正确答案

（1）（2）

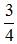
解析

（1）解：由题意得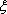的分布列为

则

（2）解：由（1）知，获得1等奖或2等奖的概率为

由题意得

则

知识点

两条直线平行的判定

题型：填空题

填空题 · 5 分

若函数f（x）=cos2x+asinx在区间（，）是减函数，则a的取值范围是　_________　。

正确答案

（﹣∞，2]

解析

由f（x）=cos2x+asinx

=﹣2sin2x+asinx+1，

令t=sinx，

则原函数化为y=﹣2t2+at+1。

∵x∈（，）时f（x）为减函数，

则y=﹣2t2+at+1在t∈（，1）上为减函数，

∵y=﹣2t2+at+1的图象开口向下，且对称轴方程为t=。

∴，解得：a≤2。

∴a的取值范围是（﹣∞，2]。

知识点

两条直线平行的判定

题型：单选题

单选题 · 5 分

设函数的图像关于直线对称，它的周期是，则（）

A的图象过点

B在上是减函数

C的一个对称中心是

D将的图象向右平移个单位得到函数的图象。

正确答案

解析

略。

知识点

两条直线平行的判定

题型：简答题

简答题 · 14 分

在四棱锥中，底面是正方形，为的中点.

（1）求证：∥平面；

（2）求证：；

（3）若在线段上是否存在点，使？若存在，求出的值，若不存在，请说明理由。

正确答案

见解析

解析

（1）连接.

由是正方形可知,点为中点.

又为的中点，

所以∥………………….2分

又

所以∥平面………….4分

（2）证明：由

所以

由是正方形可知,

又

所以………………………………..8分

又

所以…………………………………………..9分

（3）解法一：

在线段上存在点，使. 理由如下：

如图，取中点，连接.

在四棱锥中，，

所以.…………………………………………………………………..11分

由（2）可知，而

所以，

因为

所以…………………………………………………………. 13分

故在线段上存在点，使.

由为中点，得…………………………………………… 14分

解法二：

由且底面是正方形，如图，

建立空间直角坐标系

由已知设，

则

设为线段上一点，且，则

…………………………..12分

由题意，若线段上存在点，使，则，.

所以，，

故在线段上存在点，使，且…………………… 14分

知识点

两条直线平行的判定

题型：单选题

单选题 · 5 分

5．“”是“直线:与:平行”的（）

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定两条直线平行的判定

继续学习学习下一知识点

下一知识点 : 两条直线平行与倾斜角、斜率的关系

百度题库 > 高考 > 理科数学 > 两条直线平行的判定

扫码查看完整答案与解析