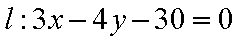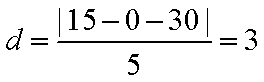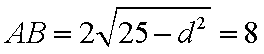- 圆的标准方程
- 共116题
如图,





求证:
正确答案
见解析。
解析
因为



所以
故直角三角形

则

知识点
如图,AB是半圆O的直径,C是圆周上一点(异于A、B),过C作圆O的切线

正确答案
见解析
解析
证明:连结

因为


所以
又因为
所以
又因为直线


又

所以
知识点
在平面直角坐标系xOy中,圆的参数方程为
(1)圆的直角坐标方程;
(2)圆的极坐标方程。
正确答案
见解析。
解析
(1)由

①2+②2得:(x﹣2)2+y2=4。
∴圆的直角坐标方程为(x﹣2)2+y2=4;
(2)把
得(ρcosθ﹣2)2+(ρsinθ)2=4,
整理得,ρ2﹣4ρcosθ=0,
∴ρ=0(舍)或ρ=4cosθ。
∴圆的极坐标方程为ρ=4cosθ。
知识点
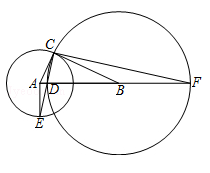
几何证明选讲:如图,已知圆A,圆B都经过点C,BC是圆A的切线,圆B交AB于点D,连结CD并延长交圆A于点E,连结AE,求证DE•DC=2AD•DB。
正确答案
见解析
解析
证明:
∵BC是⊙A的切线,∴AC⊥BC,
∵∠ACD+∠BCD=90°,AC=AE,BC=BD,
∴∠ACD=∠E,∠BCD=∠BDC,
∵∠ADE=∠BDC,∴∠E+∠ADE=90°,
∴AE⊥AB。
延长DB交⊙B于点F,连接FC,则DF=2DB,∠DCF=90°,
∴∠ACD=∠F,∴∠E=∠F,∴Rt△ADE∽Rt△CDF,
∴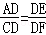
∵DF=2DB,
∴DE•DC=2AD•DB。
知识点
在极坐标系中,圆C: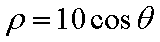
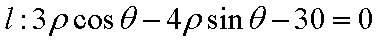
正确答案
见解析
解析
分别将圆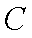
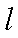
圆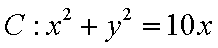

直线
因为圆心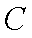
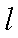
所以
知识点
扫码查看完整答案与解析