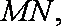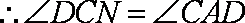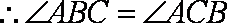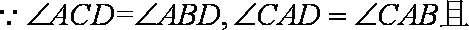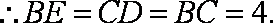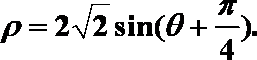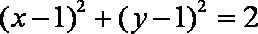- 圆的标准方程
- 共116题
选修4—1:几何证明选讲
如图

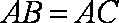
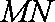

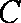
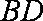
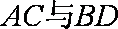

(1)求证: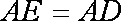
(2)若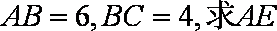
正确答案
见解析。
解析
(1)证明:
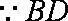
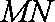
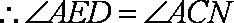
又

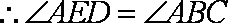
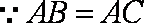
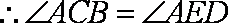
又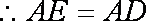

(2) 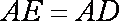
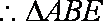
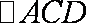
设
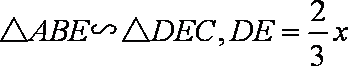
又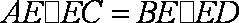
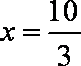

知识点
如图,椭圆方程为












(1)求

(2)已知







正确答案
见解析
解析
解析:(1)当点P不在










当点P在



(2)连结OE,易知轨迹T上有两个点

分别过A,B作直线OE的两条平行线

∴符合条件的点均在直线

∵




………………………………………………………………………………………8分
设点



分别解
得

∵



在

∴满足条件的点

知识点
如图,以△ABC的边AB为直径的半圆交AC于点D,交BC于点E,EF⊥AB于点F,AF=3BF,BE=2EC=2.那么CD= 。
正确答案
解析
连结AE,OE,O是圆的圆心,因为AB是圆的直径,所以AE⊥BC,
又AF=3BF,EF⊥AB,所以△OBE是正三角形,BE=2EC=2.所以圆的半径为2,
AE=



CA与CB是圆的割线,所以CD•CA=CE•CB,



故答案为:
知识点
如图,已知椭圆Γ:+=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足||=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足·=0,||≠0.
(1)求点M的轨迹C的方程;
(2)设不过原点O的直线l与轨迹C交于A,B两点,若直线OA,AB,OB的斜率依次成等比数列,求△OAB面积的取值范围;
(3)由(2)求解的结果,试对椭圆Γ写出类似的命题.(只需写出类似的命题,不必说明理由)
正确答案
见解析
解析
解:(1)设M(x,y)为轨迹C上的任意一点.
当||=0时,点(a,0)和点(-a,0)在轨迹C上.
当||≠0且||≠0时,由·=0,得⊥.
又||=||(如图),所以M为线段F2Q的中点.
在△QF1F2中,||=||=a,所以有x2+y2=a2.
综上所述,点M的轨迹C的方程是x2+y2=a2.…………………………(4分)
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),A(x1,y1),B(x2,y2),
由消去y并整理,得
(1+k2)x2+2kmx+m2-a2=0,
则△=4k2m2-4(1+k2)(m2-a2)=4(k2a2+a2-m2)>0,
且x1+x2=,x1x2=.
∴y1 y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
∵直线OA,AB,OB的斜率依次成等比数列,
∴·==k2,
即+m2=0,又m≠0,
∴k2=1,即k=±1.
∴S△OAB=|AB|d=|x1-x2 |·
=|x1-x2 ||m|=
由直线OA,OB的斜率存在,且△>0,得0<m2<2a2且m2≠a2,
∴
故△OAB面积的取值范围为(0,a2).…………………………………(10分)
(3)对椭圆Γ而言,有如下类似的命题:“设不过原点O的直线l与椭圆Γ交于A,B两点,若直线OA,AB,OB的斜率依次成等比数列,则△OAB面积的取值范围为(0,ab).”(13分)
知识点
选修4—4:坐标系与参数方程选讲
在直角坐标系
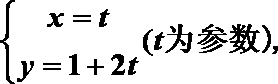
(1)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;
(2)判断直线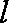
正确答案
答案:见解析。
解析
(1)将直线
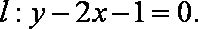
由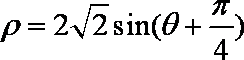
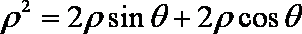
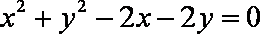
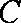

(2)由(1)知,圆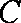
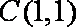
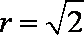

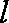

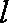

知识点
扫码查看完整答案与解析