- 圆锥曲线与方程
- 共2626题
8. 设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数






(1)试求
(2)求
(3)证明:当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
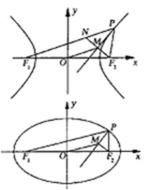
16.如图,P是双曲线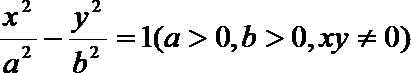
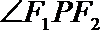
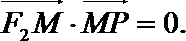
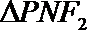
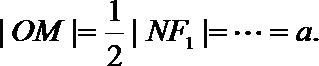
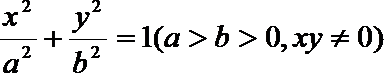
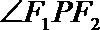
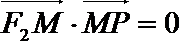
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,已知椭圆





(Ⅰ)设直线




(Ⅱ)是否存在常数


正确答案
(Ⅰ)设

因为点P在双曲线

因此

(Ⅱ)由于PF1的方程为

得
所以
同理可得

又
故
因此,存在

解析
解析已在路上飞奔,马上就到!
知识点
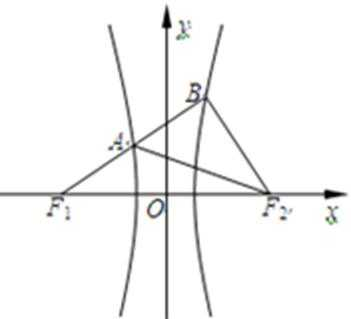
10.如图,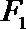
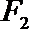
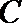
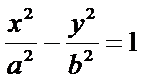
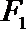
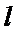
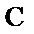
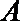
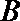
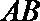
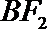
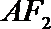
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14 - 15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,曲线

15.(几何证明选讲选做题)
如图,








正确答案
14. 2
15. 3
解析
解析已在路上飞奔,马上就到!
知识点
16.过双曲线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知双曲线







正确答案
解析
知识点
4.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆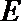
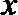
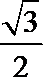
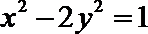
(Ⅰ)求椭圆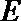
(Ⅱ)命题:“设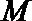
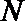
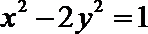
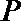
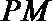
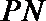

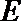
(Ⅲ)试推广(Ⅱ)中的命题,写出关于方程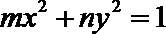
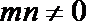

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析