- 圆锥曲线与方程
- 共2626题
13.双曲线 
正确答案
2
知识点
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
双曲线




(1)若


(2)设



正确答案
知识点
3.在平面直角坐标系xOy中,双曲线
正确答案
知识点
已知F1,F2是双曲线E: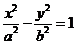
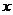
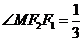
正确答案
知识点
21.(本题满分14分)本题共2个小题,第1小题满分6分,第2小题满分8分
双曲线





(1) 若


(2) 设



正确答案
(1)由已知
取
∵
∴
即
∴
∴渐近线方程为
(2)若
∴
设



∴

∵
∴
∴代入(*)式,可得
直线
∴
设直线

得
∴
∴
∴
∴直线
知识点
7.已知椭圆



正确答案
解析
.由题意知




考查方向
解题思路
根据焦点重合找出m,n的关系,

易错点
离心率之积的判断会出错。
知识点
5.已知方程
正确答案
知识点
13.已知双曲线E1:
正确答案
2
知识点
11.已知


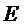
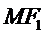
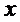
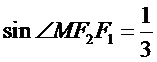
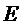
正确答案
解析
A
离心率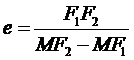

故选A.
考查方向
解题思路
根据双曲线的定义及正弦定理直接计算即可。
易错点
不能准确区分双曲线中a,b,c的关系与椭圆中a,b,c的关系导致出错。
知识点
(2015•上海)已知点 P和Q的横坐标相同,P的纵坐标是Q的纵坐标的2倍,P和Q的轨迹分别为双曲线C1和C2.若C1的渐近线方程为y=±
正确答案
知识点
6.若圆锥的侧面积与过轴的截面面积之比为
正确答案
解析
由题意得:

考查方向
解题思路
掌握对应几何体的侧面积,轴截面面积计算方法.如 圆柱的侧面积 




易错点
几何体的空间结构
知识点
9.已知点











正确答案
解析
由题意得:





考查方向
解题思路
(1)已知渐近线方程y=mx,若焦点位置不明确要分





易错点
双曲线焦点所在坐标轴
知识点
3.若双曲线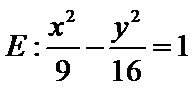
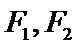
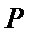
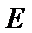
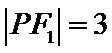

正确答案
解析
由双曲线定义得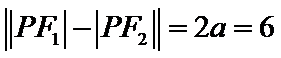
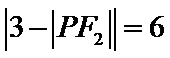
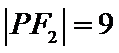
考查方向
解题思路
确定P在双曲线的左支上,由双曲线的定义可得结论。
易错点
计算能力弱,双曲线焦点坐标不会求
知识点
6.若双曲线
正确答案
解析
由题意得


考查方向
解题思路
直接根据题意得到a,b,c之间的关系即可得到答案。
易错点
弄错渐近线方程导致结果出错。
知识点
10.已知双曲线


正确答案
解析
将


考查方向
解题思路
本题考查运用双曲线的渐近线方程及抛物线的准线方程,求a,b,解题步骤如下:将



易错点
本题必须注意审题,忽视则会出现错误。
知识点
扫码查看完整答案与解析