圆锥曲线与方程_章节学习

1

题型：填空题

|

填空题 · 5 分

抛物线的焦点坐标为，则抛物线的方程为，若点在抛物线上运动，点在直线上运动，则的最小值等于（） .

正确答案

解析

略

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 14 分

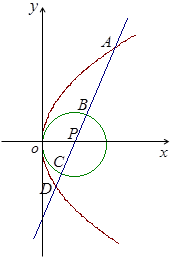
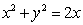
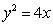
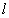
给定圆P:及抛物线S:,过圆心作直线,此直线与上述两曲线

的四个交点,自上而下顺次记为,如果线段的长按此顺序构成一个等差数列,求直线的方程。

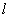
正确答案

见解析。

解析

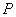
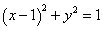
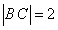
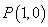
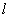
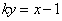
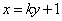
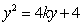
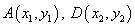
圆的方程为,则其直径长,圆心为,设的方程为,即,代入抛物线方程得:,设，

有,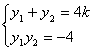

则.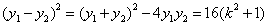

故

,

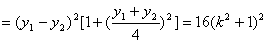
因此.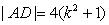

据等差,,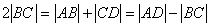

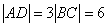
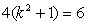
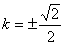
所以，即,，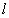

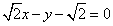
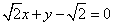
即：方程为或.

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

是抛物线的焦点，过焦点且倾斜角为的直线交抛物线于两点，设，则：①若且，则的值为；②（用和表示）.

正确答案

① ；②或

解析

略

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

已知是曲线的焦点，，则的值是。

正确答案

解析

略

知识点

抛物线的定义及应用参数方程化成普通方程抛物线的参数方程

1

题型：填空题

|

填空题 · 5 分

已知点P在抛物线y2=4x上，那么点P到点Q（2，﹣1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为　　。

正确答案

解析

∵y2=4x

∴p=2，焦点坐标为（1，0）

依题意可知当P，Q和焦点三点共线且点P在中间的时候，距离之和最小如图，

故P的纵坐标为﹣1，然后代入抛物线方程求得x=，

故答案为：（，﹣1）。

知识点

抛物线的定义及应用

1

题型：单选题

|

单选题 · 5 分

设抛物线的顶点在原点,准线方程为则抛物线的方程是( )

A

B

C

D

正确答案

B

解析

∵准线方程为x=-2

∴=2

∴p=4

∴抛物线的方程为y2=8x

故选B

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 4 分

平面直角坐标系中，方程的曲线围成的封闭图形绕轴旋转一周所形成的几何体的体积为。

正确答案

解析

略

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

曲线是平面内到定点的距离与到定直线的距离之和为3的动点的轨迹. 则曲线与轴交点的坐标是（）；又已知点（为常数），那么的最小值=（） .

正确答案

解析

略

知识点

抛物线的定义及应用抛物线的标准方程和几何性质定义法求轨迹方程

1

题型：填空题

|

填空题 · 5 分

在平面直角坐标系中，直线（）与抛物线所围成的封闭图形的面积为，则。

正确答案

2

解析

略

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

抛物线的准线方程为；经过此抛物线的焦点是和点，且与准线相切的圆共有个。

正确答案

， 2

解析

略

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 18 分

（1）设椭圆：与双曲线：有相同的焦点，是椭圆与双曲线的公共点，且的周长为，求椭圆的方程；

我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.

（2）如图，已知“盾圆”的方程为.设“盾圆”上的任意一点到的距离为，到直线的距离为，求证：为定值；

（3）由抛物线弧：（）与第（1）小题椭圆弧：（）所合成的封闭曲线为“盾圆”.设过点的直线与“盾圆”交于两点，，且（），试用表示；并求的取值范围.

正确答案

见解析

解析

（1）由的周长为得，

椭圆与双曲线：有相同的焦点，所以，

即，，椭圆的方程；…………………4分

（2）证明：设“盾圆”上的任意一点的坐标为，.………5分

当时，，，

即；…………………………7分

当时，，，

即；…………………………9分

所以为定值；…………………………………………………………10分

（3）显然“盾圆”由两部分合成，所以按在抛物线弧或椭圆弧上加以分类，由“盾圆”的对称性，不妨设在轴上方（或轴上）：

当时，，此时，；……………………11分

当时，在椭圆弧上，

由题设知代入得，

，

整理得，

解得或（舍去）. …………………………………12分

当时在抛物线弧上，

由方程或定义均可得到，于是，

综上，（）或（）；

相应地，，…………………………………………14分

当时在抛物线弧上，在椭圆弧上，

；……………………15分

当时在椭圆弧上，在抛物线弧上，

；……………………16分

当时、在椭圆弧上，

；…………………………17分

综上的取值范围是.…………………………………………………18分

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 16 分

设抛物线的焦点为，经过点的动直线交抛物线于

两点，且。

（1）求抛物线的方程；

（2）若为坐标原点），且点在抛物线上，求直线的倾斜角；

（3）若点是抛物线的准线上的一点，直线的斜率分别为，求证：当为定值时，也为定值。

正确答案

见解析

解析

（1）设直线的方程为，代入，可得

（*）

由是直线与抛物线的两交点，

故是方程（*）的两个实根， ……………………2分

∴，又，所以，又，可得

所以抛物线的方程为，　　　　　　　　　　　　　 ……………………4分

【另法提示：考虑直线l垂直于x轴这一特殊情形，或设直线l方程为点斜式】

（2）由（1）可知，

∵，∴

………………………7分

又点在抛物线上，故，

即，可得，即，

设直线的倾斜角为，则，又，

故直线的倾斜角为或，　　　　　………………………10分

【另法提示：设直线l方程为点斜式】

（3），可得， ………………………11分

由（2）知又，

∴

………………………14分

，又为定值，

所以也为定值

知识点

抛物线的定义及应用

1

题型：填空题

|

填空题 · 5 分

已知抛物线上一点到其焦点的距离为5，该抛物线的顶点到直线MF的距离为d，则d的值为　　。

正确答案

解析

略

知识点

抛物线的定义及应用

1

题型：简答题

|

简答题 · 16 分

设抛物线的焦点为，经过点的动直线交抛物线于点
，且.

（1）求抛物线的方程；

（2）若(为坐标原点)，且点在抛物线上，求直线倾斜角；

（3）若点是抛物线的准线上的一点，直线的斜率分别为.求证：当为定值时，也为定值.

正确答案

见解析

解析

解析：

（1）根据题意可知：，设直线的方程为：，则：

联立方程：，消去可得：（*），

根据韦达定理可得：，∴，∴：

（2）设，则：，由（*）式可得：

∴，

又，∴

∴

∵，∴，∴，∴

∴直线的斜率，∴倾斜角为或

（3）可以验证该定值为，证明如下：

设，则：，，

∵，∴

∴

∴为定值

知识点

抛物线的定义及应用

1

题型：单选题

|

单选题 · 5 分

过抛物线的焦点作一条直线与抛物线相交于两点,它们到直线的距离之和等于5，则这样的直线

A有且仅有一条

B有且仅有两条

C有无穷多条

D不存在

正确答案

D

解析

略

知识点

抛物线的定义及应用

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点