- 圆锥曲线与方程
- 共2626题
设抛物线





(1)求抛物线
(2)设






(3)①对给定的定点






②对





正确答案
见解析
解析
(1)由条件得


……………………………. 4分
(2)直线方程为


设






……………………………. 8分
因此
综上得
……………………………. 10分
(3)①设过



设





设存在直线





②当

当

知识点
过抛物线



正确答案
解析
根据题意设













知识点
由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱。1个单位的固体碱在水中逐步溶化,水中的碱浓度


(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二

正确答案
见解析
解析
(1)



即若1个单位的固体碱只投放一次,则能够维持有效抑制作用的时间为
(2)当

当

所以当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,
即

故当且仅当


知识点
如图,过坐标原点




























(1)求
(2)求

(3)设








正确答案
(1)


解析
解析:(1)如图,由







同理


(2)如图,法1:点






消去

又
从而
由①有
②-①得
即

所以





法2:点


所以直线

因此,点



又


以下各步同法1
法3:
点

即点

又

即
以下各步同法1
(3)因为
知识点
已知抛物线y2=6x上的两个动点A(x1,y1)和B(x2,y2),其中




(1)试证直线
(2)设


(3)求⊿ABC面积的最大值。
正确答案
见解析
解析
设线段



线段

易知





由(1)知直线


(2)代入


依题意,

所以


定点



………………11分
当且仅当



所以,

知识点
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点PA⊥l,A为垂足,如果AF的斜率为-
正确答案
8
解析
抛物线的焦点为F(2,0),准线为x=-2,因为PA⊥准线l,设P(m,n),则
A(-2,n),因为AF的斜率为-





知识点
已知斜率为2的直线


正确答案
解析
抛物线的焦点坐标是










知识点
已知点A是抛物线y2=2px(p>0)上一点,F为抛物线的焦点,准线l与x轴交于点K,已知|AK|=
(1)求p的值;
(2)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦
的中点分别为G,H.求|GH|的最小值。
正确答案
(1)4(2)8
解析
解析:(1)设
因为抛物线的焦点
则


又
(2)由



设



由 


=

所以
知识点
已知直线



(1)求实数
(2)问点


正确答案
见解析。
解析
(1)将


由△

另一方面,弦长AB

(2)当

则只须使得
即

知识点
过抛物线







正确答案
1
解析
设








知识点
设斜率为1的直线l过抛物线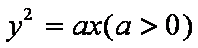
正确答案
16
解析
依题意,有F(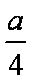
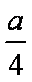
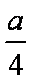
△OAF的面积为: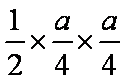
知识点
设抛物线y2=4x上一点P到直线x=-2的距离为5,则点P到该抛物线焦点的距离是
正确答案
4
解析
由抛物线的定义知:点P到抛物线焦点的距离等于点P到准线x=-1的距离,所以点P到该抛物线焦点的距离是5-1=4.
知识点
设顶点在原点,焦点在x轴上的抛物线过点P(2,4),过P作抛物线的动弦PA,PB,并设它们的斜率分别为kPA,kPB。
(1)求抛物线的方程;
(2)若kPA+kPB=0,求证直线AB的斜率为定值,并求出其值;
(3)若kPA·kPB=1,求证直线AB恒过定点,并求出其坐标。
正确答案
见解析。
解析
(1)依题意,可设所求抛物线的方程为y2=2px(p>0),
因抛物线过点(2,4),故42=4p,p=4,抛物线方程为y2=8x。
(2)设A(x1,y1),B(x2,y2),则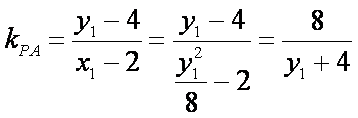
同理
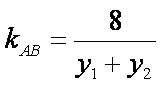
∵kPA+kPB=0,
∴



∴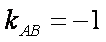
即直线AB的斜率恒为定值,且值为-1。
(3)∵kPAkPB=1,∴

直线AB的方程为
将-y1y2=4(y1+y2)-48代入上式得
(y1+y2)(y+4)=8(x+6),该直线恒过定点(-6,-4),命题得证。
知识点
已知抛物线


正确答案
解析
依题意,得F(p,0),因为AF







知识点
已知抛物线




正确答案
解析
抛物线












知识点
扫码查看完整答案与解析






















































