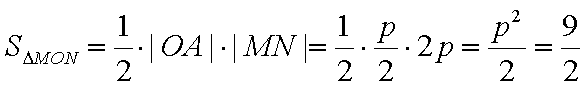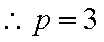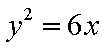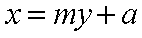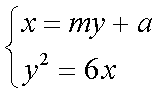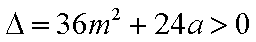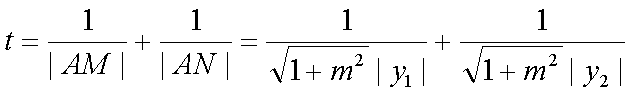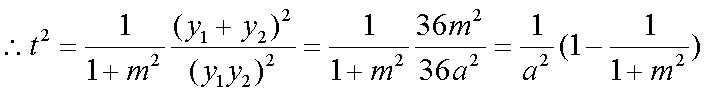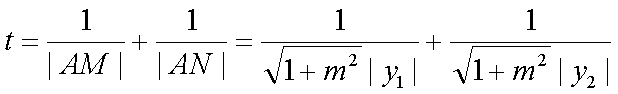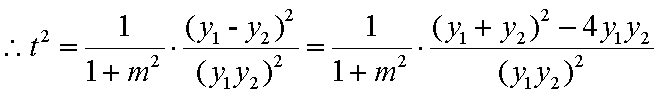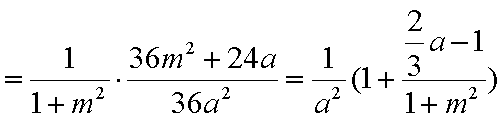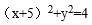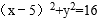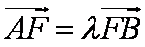- 圆锥曲线与方程
- 共2626题
己知抛物线的参数方程为









正确答案
2
解析
∵





由抛物线得几何性质得



知识点
已知P,Q为抛物线

正确答案
-4
解析
因为点P,Q的横坐标分别为4,
由




知识点
设




(1)求抛物线
(2)

















正确答案
(1)y2=4x(2)4
解析
(1)设

则



所以


(2)设


则


所以
设AC所在直线方程为
联立


同理

所以
设AB所在直线方程为


所以 
知识点
过抛物线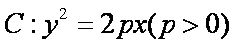
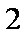


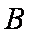
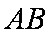
直径的圆与
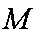
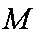
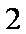
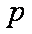
正确答案
解析
略
知识点
已知抛物C的标准方程为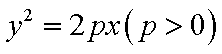

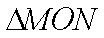
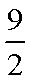
(1)求抛物线C的标准方程;
(2)记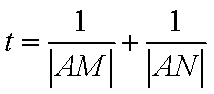
正确答案
见解析
解析
(1)由题意,
抛物线C的方程为
(2) 设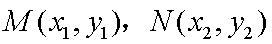
联立
得
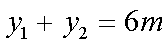
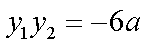
由对称性,不妨设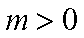
(i)
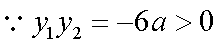
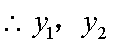
又
不论a取何值,t均与m有关,即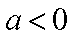
(ii) 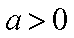
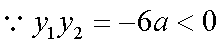
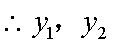
又
所以,仅当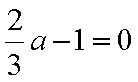
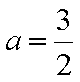
知识点
设抛物线y2=2px(p>0)的焦点为F,其准线与x轴交于点C,过点F作它的弦AB,若∠CBF=90°,则|AF|﹣|BF|= 。
正确答案
2P
解析
设AB方程为:y=k(x﹣

即k2x2﹣(k2+2)px+
设两交点为A(x2,y2),B(x1,y1),∠CBF=90°即(x1﹣

∴ x12+y12=



∴ B(



∵ x1x2=

∴ x2=
∴ A(


∴|AF|﹣|BF|=2P,
故答案为2P。
知识点
如图,直线y=2x与抛物线y=3﹣x2所围成的阴影部分的面积是( )
正确答案
解析
由

∴直线y=2x与抛物线y=3﹣x2交于点A(﹣3,﹣6)和B(1,2)
∴两图象围成的阴影部分的面积为
=(3×1﹣

=
知识点
以抛物线y2=20x的焦点为圆心,且与双曲线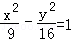
正确答案
解析
由双曲线方程可得a=3,b=4,c=5,
实轴长=6,离心率e=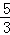
顶点坐标(﹣3,0),(3,0),
焦点坐标(﹣5,0),(5,0),
渐近线方程y=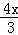
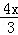
圆心(5,0)到直线4x+3y=0的距离即为所求圆的半径R
R=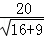
所以圆方程:(x﹣5)2+y2=16。
知识点
已知









(1)求椭圆
(2)直线






正确答案
见解析。
解析
(1)由题意可设椭圆


由题意知


故椭圆


(2)以

证明如下:由题意可设直线

则点




由

设点


所以

因为点

当




直线



当


所以直线

点


又因为

故以

综上得,当直线



知识点
抛物线







正确答案
解析
设


知识点
已知抛物线














(1)求证:

(2)若











正确答案
见解析
解析
解析:(1)设


所以



所以







(2)设

由
同理
所以面积
设

由


得到

②得

所以当


所以当




所以

知识点
过抛物线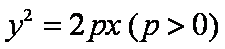
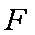
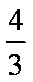
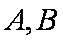
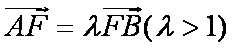
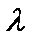
正确答案
解析
据题意设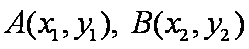
由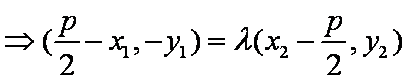
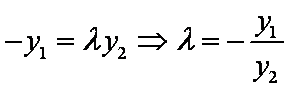
联立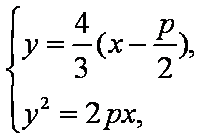
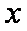
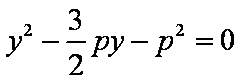
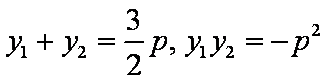
∴
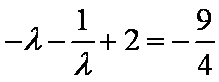
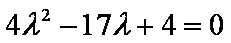
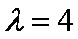
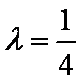
知识点
如图,已知抛物线



(1)求抛物线
(2)过点







正确答案
见解析
解析
(1)

所以

故


(2)设


则

所以

同理,




即
由


所以直线

于是
令


所以,

知识点
如图,设椭圆




(1)若抛物线上存在点

(2)若





正确答案
见解析
解析
(1)
由四边形
得
且


所以椭圆方程为
(2)
不妨设

因为
所以


又因为直线



所以

联立方程组


所以点

所以
又


知识点
已知动圆的圆心C在抛物线x2=2py(p>0)上,该圆经过点A(0,p),且与x轴交于两点M、N,则sin∠MCN的最大值为 。
正确答案
1
解析
解析 : 由题意,设C(x0,y0),则⊙C的方程(x﹣x0)2+(y﹣y0)2=x02+(y0﹣p)2。
把y=0和x02=2py0代入整理得x2﹣2x0x+x02+p2=0。
设M、N的横坐标分别为x1、x2,则x1=x0﹣p,x2=x0+p,∴|MN|=|x1﹣x2|=2p。
∵|CM|=|CN|=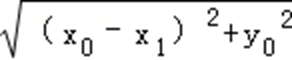
∴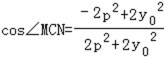

∵ 0<∠MCN<π∴ 0<sin∠MCN≤1,
∴ sin∠MCN的最大值为1故答案为:1
知识点
扫码查看完整答案与解析