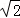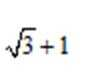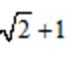- 圆锥曲线与方程
- 共2626题
若抛物线
A
B
C
D
正确答案
解析
焦点坐标
知识点
10.抛物线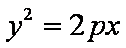
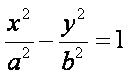
A
B
C
D
正确答案
解析
因为抛物线和双曲线焦点相同，所以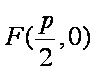
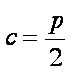
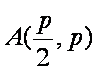
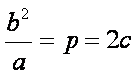
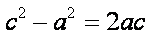
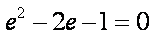
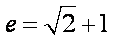
知识点
抛物线
正确答案
解析
知识点
已知抛物线Γ：y2=4x的焦点为F，P是Γ的准线上一点，Q是直线PF与Γ的一个交点，若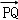
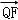
正确答案
x+y﹣1=0或x﹣y﹣1=0
解析
抛物线Γ：y2=4x的焦点F（1，0），设Q到l的距离为d，则|QF|=d
∵
∴|
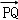
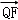
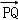
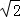
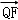
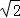
∴直线的倾斜角为45°或135°，
∴直线的斜率为±1，
∴直线的方程为x+y﹣1=0或x﹣y﹣1=0。
故答案为：x+y﹣1=0或x﹣y﹣1=0。
知识点
9.抛物线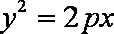
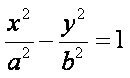
A
B
C
D
正确答案
解析
因为抛物线和双曲线焦点相同，所以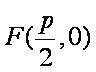
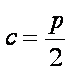
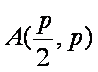
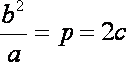
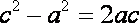
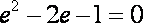
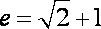
知识点
13.过抛物线
正确答案
2
解析
由题意可知过焦点的直线方程为
知识点
14.已知抛物线方程为
正确答案
解析
略
知识点
10.已知抛物线C1：y=
A
B
C
D
正确答案
解析
由抛物线C1：y=
所以抛物线的焦点坐标为F（0，
由
则抛物线的焦点与双曲线的右焦点的连线所在直线方程为
即
设该直线交抛物线于M（
由题意可知
把M点代入①得：
知识点
已知抛物线的方程为
A2
B
C2或
D2或
正确答案
解析
过A作AD⊥x轴于D，令FD=m，则FA=2m，即F到准线的距离为2m，由抛物线的定义可得p+m=2m，即m=p，所以
知识点
已知抛物线
（1）求抛物线C的方程；
（2）以M点为起点的任意两条射线l1，l2的斜率乘积为l，并且l1与抛物线C交于A、B两点，l2与抛物线C交于D、E两点，线段AB、DE的中点分别为G、H两点，求证：直线GH过定点，并求出定点坐标。
正确答案
见解析
解析
解：（1）∵
又∵点N在抛物线C上，∴62=18p，解得p=2。
∴抛物线C的方程为y2=4x。
2）由题意可知：直线l1，l2的斜率存在且不为0，
设l1：y=k（x﹣12）+8，则l2：
由
是A（x1，y1），B（x2，y2），则
又y1+y2=k（x1+x2﹣24）+16，
∴x1+x2=
∴线段AB的中点G
用
∴kGH=
∴直线GH：
令y=0，得到x=10。
∴直线GH过定点（10，0）。
知识点
正确答案
（0,2）
解析
略
知识点
10.已知抛物线
A
B
C3
D2
正确答案
解析
设
知识点
正确答案
（0,2）
解析
略
知识点
3．下表提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对应数据．根据下表提供的数据，求出y关于x的线性回归方程为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6. 抛物线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析